题目内容
3.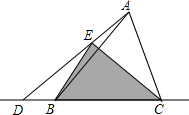 如图,D是给定△ABC边BC所在直线上一动点,E是线段AD上一点,DE=2AE,连接BE,CE,点D从B的左边开始沿着BC方向运动,则△BCE的面积变换情况是( )
如图,D是给定△ABC边BC所在直线上一动点,E是线段AD上一点,DE=2AE,连接BE,CE,点D从B的左边开始沿着BC方向运动,则△BCE的面积变换情况是( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 先变小后变大 | D. | 始终不变 |
分析 过点E作EF⊥BC于F,过点A作AG⊥BC于G,根据相似三角形对应边成比例用AG表示出EF,再根据三角形的面积公式解答.
解答  解:如图,过点E作EF⊥BC于F,过点A作AG⊥BC于G,
解:如图,过点E作EF⊥BC于F,过点A作AG⊥BC于G,
则EF∥AG,
所以,△ADG∽△EDF,
所以,$\frac{AD}{DE}$=$\frac{AG}{EF}$,
∵DE=2AE,
∴AD=DE+AE=3AE,
∴$\frac{3AE}{2AE}$=$\frac{AG}{EF}$,
∴EF=$\frac{2}{3}$AG,
∴△BCE的面积=$\frac{1}{2}$BC•EF=$\frac{1}{2}$BC•$\frac{2}{3}$AG=$\frac{2}{3}$×$\frac{1}{2}$BC•AG=$\frac{2}{3}$S△ABC,
∴△BCE的面积始终不变.
故选D.
点评 本题考查了三角形的面积,相似三角形的判定与性质,作辅助线构造出相似三角形并表示出△BCE底边BC上的高是解题的关键.

练习册系列答案
相关题目
11.某中学为了解九年级学生的身体素质情况,随机抽查了九年级部分学生一分钟跳绳次数,绘制成如下统计图表(图1,图2,表).
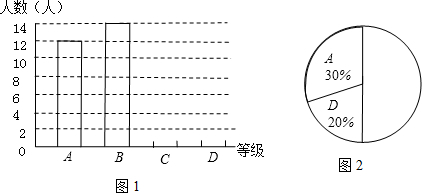
请结合图表完成下列问题:
(1)表1中a=6,b=8;
(2)请把图1和图2补充完整;
(3)已知该校有1000名九年级学生,若在一分钟内跳绳次数不大于120次的为不合格,则该校九年级学生一分钟跳绳不合格的学生估计为200人.
| 等级 | 一分钟跳 绳次数x | 人数 |
| A | x>180 | 12 |
| B | 150<x≤180 | 14 |
| C | 120<x≤150 | a |
| D | x≤120 | b |

请结合图表完成下列问题:
(1)表1中a=6,b=8;
(2)请把图1和图2补充完整;
(3)已知该校有1000名九年级学生,若在一分钟内跳绳次数不大于120次的为不合格,则该校九年级学生一分钟跳绳不合格的学生估计为200人.
 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( ) ”组成,其中第①个图案中有4个,第②个图案中有9个,第③个图案中有16个,第④个图案有25个,…,则第⑨个图案中的个数为( )
”组成,其中第①个图案中有4个,第②个图案中有9个,第③个图案中有16个,第④个图案有25个,…,则第⑨个图案中的个数为( )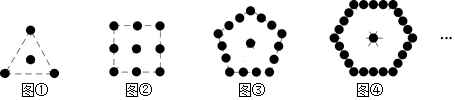
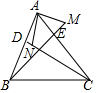 如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.
如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.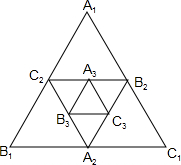 如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.
如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.