题目内容
 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=| k |
| x |
(1)求点B的坐标;
(2)求一次函数y=ax+b的表达式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先求方程x2-x-6=0的两个根,得出点A坐标,代入即可得出反比例函数的解析式,求得点B坐标即可;
(2)把点A、B代入一次函数的解析式,即可得出一次函数y=ax+b的表达式.
(2)把点A、B代入一次函数的解析式,即可得出一次函数y=ax+b的表达式.
解答:解:(1)∵x1、x2是方程x2-x-6=0的两个根,
∴(x-3)(x+2)=0,
解得x1=3,x2=-2;
∴点A坐标为(-2,-3),
代入y=
得k=6.
∴反比例函数的解析式y=
,
把x2=3代入反比例函数的解析式得y2=2,
∴点B坐标为(3,2);
(2)把点A、B代入一次函数的解析式,得
,
解得
,
∴一次函数的表达式为y=x-1.
∴(x-3)(x+2)=0,
解得x1=3,x2=-2;
∴点A坐标为(-2,-3),
代入y=
| k |
| x |
∴反比例函数的解析式y=
| 6 |
| x |
把x2=3代入反比例函数的解析式得y2=2,
∴点B坐标为(3,2);
(2)把点A、B代入一次函数的解析式,得
|
解得
|
∴一次函数的表达式为y=x-1.
点评:本题考查了反比例函数和一次函数的交点问题,以及解一元二次方程和方程组.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
下列条件能判断两个三角形全等的是( )
①两角及一边对应相等;
②两边及其夹角对应相等;
③两边及一边所对的角对应相等;
④两角及其夹边对应相等.
①两角及一边对应相等;
②两边及其夹角对应相等;
③两边及一边所对的角对应相等;
④两角及其夹边对应相等.
| A、①③ | B、②④ |
| C、②③④ | D、①②④ |
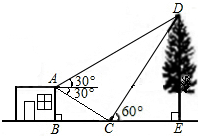 如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知平房高AB为4米,且B、C、E三点在同一条直线上,请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计).
如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知平房高AB为4米,且B、C、E三点在同一条直线上,请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计). 在平面直角坐标系中,已知A(2,0),B(3,1),C(1,3);
在平面直角坐标系中,已知A(2,0),B(3,1),C(1,3); 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤: