题目内容
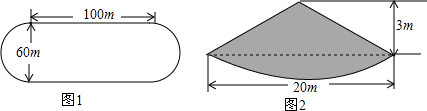
19.甲场地如图1所示,中间为一长100m,宽为60m的长方形,两边为两个半圆,现欲在甲场地上铺一层厚3m的煤,乙地为一售煤点,该售煤点有一堆近似于一个圆锥,如图2所示,该圆锥底面圆的直径为20m,高为3m.(1)甲场地需用的煤为多少立方米?乙地售煤点的这堆煤是否够用?说明理由.(π取3.14)
(2)甲地有A型货车及B型货车,A型车每辆可载煤12m3,每辆A型车的载煤体积是每辆B型车载煤体积的$\frac{3}{5}$,现甲地有A型货车10辆去乙地运煤,至少还需几辆B型货车,才能将甲地所需的煤一次从乙地运回.
(3)A型车和B型车匀速行驶在甲乙两地,A型车与B型车的速度比为4:3,一B型车从甲地出发1h后一A型车从甲地出发,沿B型车所行进的路线去乙地,B型货车到达乙地后装煤用去13min,然后原路返回与前来乙地的A型车相遇,此时这辆A型车出发21min,该A型车此时所行驶的路程比甲乙两地路程的一半多4km,求甲乙两地的路程.
分析 (1)先求得如图1和图2所示场地中煤的体积,然后比较大小即可判断;
(2)先求得一辆B型车的载重体积,然后根据A型车的载重煤的体积+B型车的载重煤的体积=乙地煤的总体积列方程求解即可;
(3)A型车的速度为每分钟4xkm,B型车的速度为每分钟3xkm.根据A型车此时所行驶的路程比甲乙两地路程的一半多4km列方程求解即可.
解答 解:(1)甲场地的面积S=3.14×302+100×60=8826m2.
则甲场地需要煤的总体积=8826×3=26478m3.
乙地有煤的体积=$\frac{1}{3}×3.14×1{0}^{2}$×3=314m3.
∵314<26478,
∴乙地的煤不够用.
(2)一辆B型车的载重体积=12÷$\frac{3}{5}$=20m3.
设需要B型车x辆,根据题意得;10×12+20x=314.
解得:x≈9.7.
∴至少需要B型车10.
答:至少需要B型车10.
(3)设A型的速度为每分钟4y千米,B型的速度为每分钟3y千米.
根据题意得;4y×21=$\frac{1}{2}×\frac{1}{2}×$(68×3y+21×4y)+4.
解得;y=$\frac{1}{3}$.
甲乙两地的路程为(4×$\frac{1}{3}×21-4$)×2=48.
答:甲乙两地的路程为48千米.
点评 本题主要考查的是一元一次方程的应用,用含y的式子表示出甲乙两地之间的距离是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
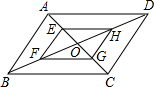 如图,在?ABCD中,对角线AC与BD相交于点O,点G、F、G、H,分别是AO,BO,CO,DO上的点.
如图,在?ABCD中,对角线AC与BD相交于点O,点G、F、G、H,分别是AO,BO,CO,DO上的点. 某城市有座古塔,现要实际测量这座古塔外墙底部的底角(图中∠ABC)的大小,请运用你所学的知识设计出测量方案,并说明理由.
某城市有座古塔,现要实际测量这座古塔外墙底部的底角(图中∠ABC)的大小,请运用你所学的知识设计出测量方案,并说明理由. 在平面直角坐标系中.
在平面直角坐标系中.