题目内容
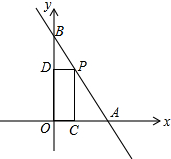 如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.点P在何处时,矩形OCPD的面积为1?
如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.点P在何处时,矩形OCPD的面积为1?考点:一次函数图象上点的坐标特征
专题:
分析:设P(a,-2a+3),则利用矩形的性质列出关于a的方程,通过解方程求得a值,继而求得点P的坐标.
解答:解:∵点P在一次函数y=-2x+3的图象上,
∴P(a,-2a+3)(a>0),
由题意得 a•(-2a+3)=1,
整理得2a2-3a+1=0,
解得 a1=1,a2=
,
∴-2a+3=1或-2a+3=2.
综上所述,当P(1,1)或(
,2)时,矩形OCPD的面积为1.
∴P(a,-2a+3)(a>0),
由题意得 a•(-2a+3)=1,
整理得2a2-3a+1=0,
解得 a1=1,a2=
| 1 |
| 2 |
∴-2a+3=1或-2a+3=2.
综上所述,当P(1,1)或(
| 1 |
| 2 |
点评:本题考查了一次函数图象上点的坐标特征.一次函数图象上所有点的坐标都满足该函数关系式.

练习册系列答案
相关题目
若等腰三角形的腰长为5cm,底长为8cm,那么腰上的高为( )
| A、12cm | B、10cm |
| C、4.8cm | D、6cm |
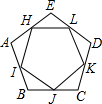 如图,H、I、J、K、L分别是正五边形ABCDE各边的中点,求证:五边形HIJKL是正五边形.
如图,H、I、J、K、L分别是正五边形ABCDE各边的中点,求证:五边形HIJKL是正五边形. 如图,等边三角形ABC,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.若CE=BF,则∠EPF=
如图,等边三角形ABC,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.若CE=BF,则∠EPF= 如图,点M把线段AB分成
如图,点M把线段AB分成 在同圆中,若
在同圆中,若