题目内容
 如图,等边三角形ABC,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.若CE=BF,则∠EPF=
如图,等边三角形ABC,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.若CE=BF,则∠EPF=考点:全等三角形的判定与性质,等边三角形的性质
专题:计算题
分析:由三角形ABC为等边三角形,利用等边三角形的性质得到三个内角为60°,三边相等,利用SAS得到三角形ABF与三角形BCE全等,利用全等三角形对应角相等得到∠BAF=∠CBE,由∠EPF为三角形BPF的外角,利用外角性质及等量代换即可求出∠EPF的度数.
解答:解:∵△ABC为等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,
在△ABF和△BCE中,
,
∴△ABF≌△BCE(SAS),
∴∠BAF=∠CBE,
∵∠EPF为△BPF的外角,
∴∠EPF=∠CBE+∠AFB=∠BAF+∠AFB=120°.
故答案为:120°.
∴∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,
在△ABF和△BCE中,
|
∴△ABF≌△BCE(SAS),
∴∠BAF=∠CBE,
∵∠EPF为△BPF的外角,
∴∠EPF=∠CBE+∠AFB=∠BAF+∠AFB=120°.
故答案为:120°.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
计算:
①0.25-
+(-1
)-(+3
)
②-105
÷(-
)
③-32+(-2
)2×(-
)+|-22|
④(-1)2013-{(-3)3-[3+
×(-1
)]÷(-2)}.
①0.25-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
②-105
| 5 |
| 9 |
| 5 |
| 3 |
③-32+(-2
| 1 |
| 2 |
| 4 |
| 25 |
④(-1)2013-{(-3)3-[3+
| 2 |
| 3 |
| 1 |
| 2 |
在Rt△ABC中,∠C=90°,若sinA=
,则cosB的值是( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法:①0是整数;②4.2不是正数;③自然数一定是正数;④-2.5是负分数;⑤负分数一定是负有理数.其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
一种面粉包装袋上的质量标识为“25±0.5kg”,则下列四袋面粉中不合格的是( )
| A、24.5kg |
| B、25.5kg |
| C、24.8kg |
| D、26.1kg |
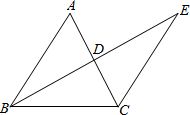 如图,BE⊥AC,垂足为D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=
如图,BE⊥AC,垂足为D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=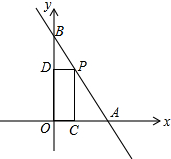 如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.点P在何处时,矩形OCPD的面积为1?
如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.点P在何处时,矩形OCPD的面积为1?