题目内容
若等腰三角形的腰长为5cm,底长为8cm,那么腰上的高为( )
| A、12cm | B、10cm |
| C、4.8cm | D、6cm |
考点:等腰三角形的性质,勾股定理
专题:
分析:可以作出底边上的高,且易求出底边上的高为3cm,再利用等积法可求得腰上的高.
解答: 解:如图,△ABC中,AB=AC=5cm,BC=8cm,过点A作AD⊥BC,交BC于点D,
解:如图,△ABC中,AB=AC=5cm,BC=8cm,过点A作AD⊥BC,交BC于点D,
则BD=
BC=4cm,在Rt△ABD中,由勾股定理可求得AD=3cm,
设腰上的高为h,则
BC•AD=
AB•h,
即
×8×3=
×5•h,
解得h=4.8cm.
故选C.
 解:如图,△ABC中,AB=AC=5cm,BC=8cm,过点A作AD⊥BC,交BC于点D,
解:如图,△ABC中,AB=AC=5cm,BC=8cm,过点A作AD⊥BC,交BC于点D,则BD=
| 1 |
| 2 |
设腰上的高为h,则
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得h=4.8cm.
故选C.
点评:本题主要考查等腰三角形的性质,在解题中等积法的应用可以起到事半功倍的效果.

练习册系列答案
相关题目
 如图,小李打网球时,球恰好打过网,且落在离网4m的位置上,则球拍击球的高度h为( )
如图,小李打网球时,球恰好打过网,且落在离网4m的位置上,则球拍击球的高度h为( )| A、1.6m | B、1.5m |
| C、2.4m | D、1.2m |
 如图,AD∥EF∥BC,则图的相似三角形的对数为( )
如图,AD∥EF∥BC,则图的相似三角形的对数为( )| A、3 | B、4 | C、5 | D、6 |
一种面粉包装袋上的质量标识为“25±0.5kg”,则下列四袋面粉中不合格的是( )
| A、24.5kg |
| B、25.5kg |
| C、24.8kg |
| D、26.1kg |
在-3,-1
,0,-
,2002各数中,是正数的有( )
| 1 |
| 2 |
| 3 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
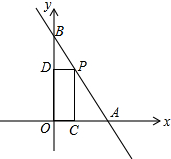 如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.点P在何处时,矩形OCPD的面积为1?
如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.点P在何处时,矩形OCPD的面积为1?