题目内容
8.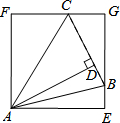 如图,△ABC中,∠BAC=45°,AD⊥BC,BD=1,CD=3,将△ABD沿AB折叠得到△ABE,将△ACD沿AC折叠得到△ACF,延长EB和FC交于点G.
如图,△ABC中,∠BAC=45°,AD⊥BC,BD=1,CD=3,将△ABD沿AB折叠得到△ABE,将△ACD沿AC折叠得到△ACF,延长EB和FC交于点G.(1)判定四边形AEGF的形状,并证明你的结论;
(2)求△ABC的面积.
分析 (1)由折叠的性质得出∠BAE=∠BAD,∠E=∠ADB=90°,AE=AD,∠FAC=∠DAC,∠F=∠ADC=90°,AF=AD,证出∠EAF=90°,得出四边形AEGF是矩形,由AE=AF,即可得出结论;
(2)设AD=x,则GF=GE=AE=x,BC=4,BG=x-1,GC=x-3,在Rt△BGC中,根据勾股定理得出方程,解方程求出AD,△ABC的面积=$\frac{1}{2}$BC×AD,即可得出结果.
解答 (1)解:四边形AEGF是正方形;理由如下:
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
由折叠的性质得:∠BAE=∠BAD,∠E=∠ADB=90°,AE=AD,
∠FAC=∠DAC,∠F=∠ADC=90°,AF=AD,
∴AE=AF,
∵∠BAC=45°,
∴∠EAF=90°,
∴四边形AEGF是矩形,
又∵AE=AF,
∴四边形AEGF是正方形;
(2)解:∵四边形AEGF是正方形,
∴∠G=90°,
设AD=x,
则GF=GE=AE=x,
由折叠的性质得:BE=BD=1,CF=CD=3,
∴BC=4,BG=x-1,GC=x-3,
在Rt△BGC中,根据勾股定理得:GC2+BG2=BC2,
即(x-3)2+(x-1)2=42,
解得:x=2±$\sqrt{7}$(负值舍去),
∴AD=2+$\sqrt{7}$,
∴△ABC的面积=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×4×(2+$\sqrt{7}$)=4+2$\sqrt{7}$.
点评 本题考查了翻折变换的性质、正方形的判定与性质、矩形的判定、勾股定理、三角形面积的计算;熟练掌握翻折变换的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
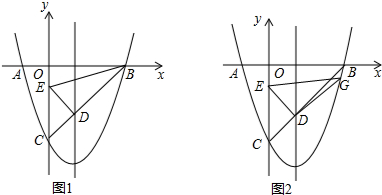
3. 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )| A. | $\frac{15}{4}$ | B. | 2 | C. | $\frac{15}{8}$ | D. | $\frac{3}{2}$ |
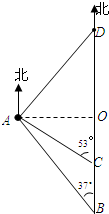 如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.