题目内容
7．在⊙O中，圆心O到弦AB的距离为AB长度的一半，则弦AB所对圆心角的大小为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 利用等腰直角三角形的性质以及垂径定理得出∠BOC的度数进而求出．
解答 
解：如图所示：连接BO，AO，
∵圆心O到弦AB的距离为AB长度的一半，
∴DO=DB，DO⊥AB，
∴∠BOD=∠B=45°，∠A=∠AOD=45°，
∴∠AOB=90°．
故选：D．
点评 此题主要考查了垂径定理以及等腰直角三角形的性质，得出∠BOD=∠B=45°，∠A=∠AOD=45°是解题关键．
练习册系列答案
相关题目
如图，点P是菱形ABCD对角线AC上的一点，连接DP并延长交AB于点E，连接BP并延长交AD于点F，交CD延长线于点G．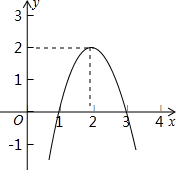
二次函数y=ax2+bx+c（a≠0）的图象如图所示，根据图象可知：方程ax2+bx+c=k有两个不相等的实数根，则k的取值范围为k＜2．
在△ABC中，∠BAC=110°，∠ACB的平分线交AB于点D，且∠CAE=40°，连接DE，则∠EDC的度数是20°．
2．sin60°=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | 1 | D． | $\frac{\sqrt{3}}{2}$ |
