题目内容
9.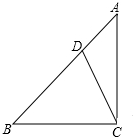 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,(1)作图:将线段CD绕点C顺时针旋转90°至CE位置,连接AE;
(2)求证:BD=AE.
分析 (1)根据题意作出线段CD绕点C顺时针旋转90°后得直线CE,然后连接AE;
(2)根据全等三角形的判定和性质即可求证.
解答 解:(1)所作图形如图所示:
(2)∵线段CE是 线段CD绕点C顺时针旋转90°后得到的,
线段CD绕点C顺时针旋转90°后得到的,
∴CE=BC,
∵∠ACB=90°,CD⊥CE,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
∵$\left\{\begin{array}{l}{CD=CE}\\{∠BCD=∠ACE}\\{BC=AC}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴BD=AE.
点评 本题考查了根据旋转变换作图以及全等三角形的判定和性质,解答本题的关键是根据题意找出条件SAS判定△BCD≌△ACE.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目




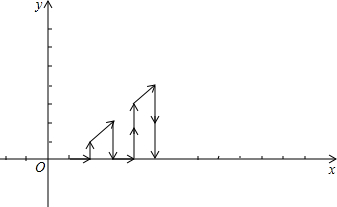 如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).
如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3). 如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G.
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G. 小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题: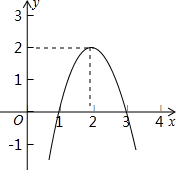 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2.