题目内容
10.解方程:(1)$\frac{5x+11}{6}$=$\frac{2x-4}{3}$;
(2)$\frac{3x+1}{2}$-2=$\frac{3x-2}{10}$-$\frac{2x+3}{5}$.
分析 首先将每个方程去分母,然后移项,合并同类项,系数化为1,求出每个方程的解各是多少即可.
解答 解:(1)去分母,可得:5x+11=2(2x-4),
去括号,得:5x+11=4x-8,
移项,合并同类项,得:x=-19.
(2)去分母,得:5(3x+1)-2×10=3x-2-2(2x+3),
去括号,得:15x+5-20=3x-2-2(2x+3),
整理,可得15x-15=-x-8,
移项,合并同类项,得:16x=7,
解得x=$\frac{7}{16}$.
点评 此题主要考查了解一元一次方程的方法,要熟练掌握,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
18.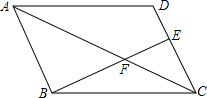 如图,在平行四边形ABCD中,E在DC边上,若DE:EC=1:2,则△CEF与△ABF的面积比为( )
如图,在平行四边形ABCD中,E在DC边上,若DE:EC=1:2,则△CEF与△ABF的面积比为( )
 如图,在平行四边形ABCD中,E在DC边上,若DE:EC=1:2,则△CEF与△ABF的面积比为( )
如图,在平行四边形ABCD中,E在DC边上,若DE:EC=1:2,则△CEF与△ABF的面积比为( )| A. | 1:4 | B. | 2:3 | C. | 4:9 | D. | 1:9 |
 如图,AB是⊙O的直径,点C在⊙O上,过点C作射线CM且满足∠ACM=∠ABC.
如图,AB是⊙O的直径,点C在⊙O上,过点C作射线CM且满足∠ACM=∠ABC. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
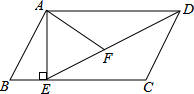 如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.