题目内容
5. 如图,AB是⊙O的直径,点C在⊙O上,过点C作射线CM且满足∠ACM=∠ABC.
如图,AB是⊙O的直径,点C在⊙O上,过点C作射线CM且满足∠ACM=∠ABC.(1)判断CM与⊙O的位置关系,并证明;
(2)延长BC到D,使BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求△ACE的外接圆的半径.$\sqrt{6}$.
分析 (1)利用圆周角定理结合等腰三角形的性质利用∠ACM=∠ABC求出答案;
(2)首先得出△AEC的外接圆的直径是AC,进而结合相似三角形的性质得出AC的长,进而得出答案.
解答 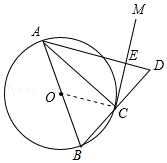 (1)证明:如图,连接OC
(1)证明:如图,连接OC
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
又∵∠ACM=∠ABC,∠OAC=∠OCA,
∴∠OCA+∠ACM=90°,
∴CM是⊙O的切线;
(2)解:∵BC=CD,
∴OC∥AD,
又∵OC⊥CE,
∴AD⊥CE,
∴△AEC是直角三角形,
∴△AEC的外接圆的直径是AC,
又∵∠ABC+∠BAC=90°,∠ACM+∠ECD=90°,
∴△ABC∽△CDE,
∴$\frac{AB}{CD}$=$\frac{BC}{ED}$,
⊙O的半径为3,
∴AB=6,
∴$\frac{6}{CD}$=$\frac{BC}{2}$,
∴BC2=12,
∴BC=2$\sqrt{3}$,
∴AC=$\sqrt{36-12}$=2$\sqrt{6}$,
∴△AEC的外接圆的半径为$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 此题主要考查了直线与圆的位置关系以及相似三角形的判定与性质,正确应用相似三角形的判定与性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在下列数-$\frac{5}{6}$,+1,6.7,-14,0,$\frac{7}{22}$,-5,25%中,属于整数的有( )
| A. | 2 个 | B. | 3 个 | C. | 4 个 | D. | 5 个 |
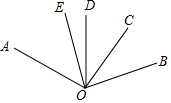 如图,OC,OD,OE是∠AOB内的射线,OD平分∠AOB,OC平分∠BOD,∠DOE=$\frac{1}{3}$∠AOE,若∠COE=45°,求∠AOB的度数.
如图,OC,OD,OE是∠AOB内的射线,OD平分∠AOB,OC平分∠BOD,∠DOE=$\frac{1}{3}$∠AOE,若∠COE=45°,求∠AOB的度数.