题目内容
9.下列运算正确的是( )| A. | x3•x2=x5 | B. | (x-1)2=x2-1 | C. | (a3)2=a9 | D. | x(x+1)=x2+1 |
分析 A、原式利用同底数幂的乘法法则计算得到结果,即可作出判断;
B、原式利用完全平方公式化简得到结果,即可作出判断;
C、原式利用幂的乘方运算法则计算得到结果,即可作出判断;
D、原式利用单项式乘以多项式法则计算得到结果,即可作出判断.
解答 解:A、原式=x5,正确;
B、原式=x2-2x+1,错误;
C、原式=a6,错误;
D、原式=x2+x,错误,
故选A.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.在过去的2015年北上广深等一线城市楼市火爆,其中仅北京的新房总成交额就达到2500亿元,若用科学记数法表示该数据应是( )
| A. | 2.5×1011元 | B. | 25×1010元 | C. | 2.5×1012元 | D. | 0.25×1011元 |
17.一次数学测试,某小组五名同学的成绩如下表(有1个数据被遮盖)
那么这五名同学成绩的方差是2分2.
| 组员 | 甲 | 乙 | 丙 | 丁 | 戊 | 平均成绩 |
| 成绩 | 91 | 89 | ★ | 90 | 92 | 90 |
4.一枚质地均匀的正方体骰子的六个面分别刻有1到6的点数,将这枚骰子掷两次,其点数之和是7的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
18.某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
| 月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?

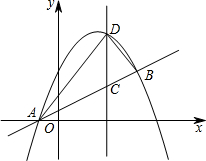 如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD. 如图所示的图形是由7个完全相同的小正方形组成的立体图形,则这个立体图形的左视图是( )
如图所示的图形是由7个完全相同的小正方形组成的立体图形,则这个立体图形的左视图是( )


