题目内容
8.观察下列各式:-1×$\frac{1}{2}$=-1+$\frac{1}{2}$
-$\frac{1}{2}$×$\frac{1}{3}$=-$\frac{1}{2}$+$\frac{1}{3}$
-$\frac{1}{3}$×$\frac{1}{4}$=-$\frac{1}{3}$+$\frac{1}{4}$…
(1)你能探索出什么规律?(用文字或表达式)
(2)试运用你发现的规律计算
(-1×$\frac{1}{2}$)+(-$\frac{1}{2}$×$\frac{1}{3}$)+(-$\frac{1}{3}$×$\frac{1}{4}$)+…+(-$\frac{1}{2013}$×$\frac{1}{2014}$)+(-$\frac{1}{2014}$×$\frac{1}{2015}$)
分析 (1)根据题目中式子的变化,可以得到式子变化的规律,从而可以解答本题;
(2)根据(1)中的规律可以解答本题.
解答 解:(1)由题意可得,
探索的规律是:$-\frac{1}{n}×\frac{1}{n+1}=-\frac{1}{n}+\frac{1}{n+1}$;
(2)(-1×$\frac{1}{2}$)+(-$\frac{1}{2}$×$\frac{1}{3}$)+(-$\frac{1}{3}$×$\frac{1}{4}$)+…+(-$\frac{1}{2013}$×$\frac{1}{2014}$)+(-$\frac{1}{2014}$×$\frac{1}{2015}$)
=$-1+\frac{1}{2}+(-\frac{1}{2})+\frac{1}{3}+(-\frac{1}{3})+\frac{1}{4}+…$+$(-\frac{1}{2013})+\frac{1}{2014}+(-\frac{1}{2014})+\frac{1}{2015}$
=-1+$\frac{1}{2015}$
=$-\frac{2014}{2015}$.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法,发现题目中式子的变化规律.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
19.若|x+y+1|+(2x-3y-2)2=0,则xy的值是( )
| A. | -$\frac{6}{25}$ | B. | $\frac{6}{25}$ | C. | $\frac{4}{25}$ | D. | -$\frac{4}{25}$ |
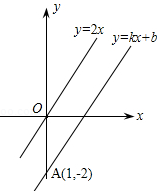 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,-2).
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,-2).