题目内容
3.计算:(1)$\sqrt{18}$-$\frac{2}{\sqrt{2}}$-$\frac{\sqrt{8}}{\sqrt{2}}$
(2)($\sqrt{24}$-$\sqrt{\frac{1}{6}}$)÷$\sqrt{3}$.
分析 (1)先约分,把二次根式化简,再合并同类二次根式;
(2)先将除法化为乘法,再根据乘法分配律进行计算.
解答 解:(1)$\sqrt{18}$-$\frac{2}{\sqrt{2}}$-$\frac{\sqrt{8}}{\sqrt{2}}$,
=3$\sqrt{2}$-$\sqrt{2}$-$\sqrt{4}$,
=2$\sqrt{2}$-2;
(2)($\sqrt{24}$-$\sqrt{\frac{1}{6}}$)÷$\sqrt{3}$,
=$\sqrt{24}$$÷\sqrt{3}$-$\sqrt{\frac{1}{6}}$$÷\sqrt{3}$,
=$\sqrt{8}$-$\sqrt{\frac{1}{6}×\frac{1}{3}}$,
=2$\sqrt{2}$-$\frac{\sqrt{2}}{6}$,
=$\frac{11\sqrt{2}}{6}$.
点评 本题考查了二次根式的混合运算:先进行二次根式的乘除运算,再把各二次根式化为最简二次根式,然后进行二次根式的加减运算.

练习册系列答案
相关题目
15.下列四个图形中,若∠1=∠2,能判断AB∥CD的是( )
| A. |  | B. |  | C. |  | D. |  |
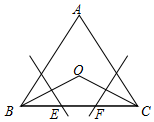 如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.
如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.