题目内容
8. 如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )
如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )| A. | AB=AC | B. | BF=EF | C. | AE=AD | D. | ∠BAE=∠CAD |
分析 先根据∠ABC=∠ACB,得出AB=AC,再根据SAS判定△ABE≌△ACD,即可得到AE=AD,∠BAE=∠CAD,据此进行判断即可.
解答 解:∵∠ABC=∠ACB,
∴AB=AC,故A选项正确;
又∵CD⊥AC于C,BE⊥AB,
∴∠ABE=∠ACD,
又∵BE=CD,
∴△ABE≌△ACD,
∴AE=AD,∠BAE=∠CAD,故C、D选项正确;
而BF=EF不一定成立.
故选:B.
点评 本题主要考查了全等三角形的判定与性质的运用,解题时注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 已知:如图,四边形ABCD中,BA<BC,BD平分∠ABC,且DA=DC.求证:∠BAD+∠BCD=180°.
已知:如图,四边形ABCD中,BA<BC,BD平分∠ABC,且DA=DC.求证:∠BAD+∠BCD=180°.
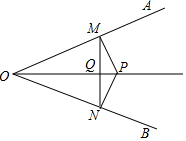 如图,点P是∠AOB角平分线OC上任一点,若过点P分别作PM⊥OA,PN⊥OB,连接MN交OP于点Q,有如下结论:
如图,点P是∠AOB角平分线OC上任一点,若过点P分别作PM⊥OA,PN⊥OB,连接MN交OP于点Q,有如下结论: 如图,已知在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于点E,EF⊥AB于点F.求证:AC=AF.
如图,已知在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于点E,EF⊥AB于点F.求证:AC=AF.