题目内容
20.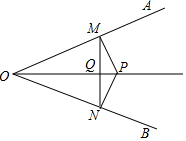 如图,点P是∠AOB角平分线OC上任一点,若过点P分别作PM⊥OA,PN⊥OB,连接MN交OP于点Q,有如下结论:
如图,点P是∠AOB角平分线OC上任一点,若过点P分别作PM⊥OA,PN⊥OB,连接MN交OP于点Q,有如下结论:(1)OM=PN,(2)PM=ON (3)MQ=NQ (4)OP⊥MN,
那么正确的结论有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 依据角平分线的性质可得到PM=PN,然后利用HL可证明Rt△OPM≌Rt△OPN,依据全等三角形的性质可证明OM=ON,最后利用等腰三角形三线合一的性质可证明③、④正确.
解答 解:∵点P是∠AOB角平分线OC上任一点,PM⊥OA,PN⊥OB,
∴PM=PN.
在Rt△OPM和Rt△OPN中$\left\{\begin{array}{l}{PM=PN}\\{OP=OP}\end{array}\right.$,
∴Rt△OPM≌Rt△OPN.
∴OM=ON.
又∵OC是∠AOB角平分线,
∴PO⊥MN,QM=QN,故③、④正确.
故选:B.
点评 本题主要考查的是全等三角形的性质和判定、角平分线的性质、等腰三角形的性质,熟练掌握相关知识是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
8. 如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )
如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )
 如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )
如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )| A. | AB=AC | B. | BF=EF | C. | AE=AD | D. | ∠BAE=∠CAD |
12.某玻璃制品销售公司职工的月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售件数),如表是甲、乙两位职工某月的工资情况.
(1)求职工的月基本保障工资和销售每件产品的奖励金额各是多少元?
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
| 职工 | 甲 | 乙 |
| 月销售件数(件) | 200 | 180 |
| 月工资(元) | 1800 | 1700 |
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
10.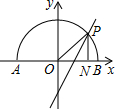 如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )
如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )
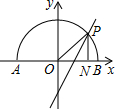 如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )
如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )| A. | (0,-1) | B. | (0,-$\frac{4}{5}$) | C. | (0,-$\frac{3}{5}$) | D. | (0,-$\frac{6}{5}$) |
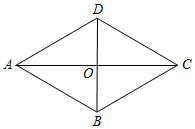 如图,菱形ABCD的面积为96,对角线AC=16,求这个菱形的周长.
如图,菱形ABCD的面积为96,对角线AC=16,求这个菱形的周长.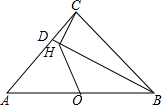 如图,△ABC中,∠ACB=90°,AC=BC=3,点D在AC上,CD=1,连接BD,过点C作CH⊥BD于点H,O为AB中点,连接OH,则OH的长为$\frac{3\sqrt{5}}{5}$.
如图,△ABC中,∠ACB=90°,AC=BC=3,点D在AC上,CD=1,连接BD,过点C作CH⊥BD于点H,O为AB中点,连接OH,则OH的长为$\frac{3\sqrt{5}}{5}$.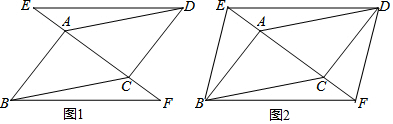
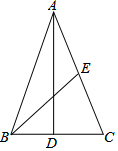 已知,如图△ABC中,AB=AC,AD⊥BC,BE是腰AC的中线,AD=12,BE=7.5,则△ABC的面积是36.
已知,如图△ABC中,AB=AC,AD⊥BC,BE是腰AC的中线,AD=12,BE=7.5,则△ABC的面积是36.