题目内容
16.已知$f(x)=\frac{1}{x(x+1)}$,则$f(1)=\frac{1}{1×(1+1)}=\frac{1}{1×2},f(2)=\frac{1}{2×(2+1)}=\frac{1}{2×3}$,那么f(1)+f(2)+f(3)+…+f(2017)=$\frac{2017}{2018}$.分析 根据拆项法,可得答案.
解答 解:原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2017}$-$\frac{1}{2018}$
=1-$\frac{1}{2018}$=$\frac{2017}{2018}$,
故答案为:$\frac{2017}{2018}$.
点评 本题考查了函数值,利用拆项法是解题关键.

练习册系列答案
相关题目
6.计算代数式(a3b2)4的结果是( )
| A. | a7b6 | B. | a7b | C. | a3b2 | D. | a12b8 |
1.已知关于x的方程x2+bx+a=0有一个根是a(a≠0),则a+b的值为( )
| A. | 2 | B. | -1 | C. | 0 | D. | 1 |
8. 如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )
如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )
 如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )
如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )| A. | AB=AC | B. | BF=EF | C. | AE=AD | D. | ∠BAE=∠CAD |
6. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=7对应的函数值y约为3.0.
②该函数的一条性质:该函数没有最大值.
 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.| x | … | 1 | 2 | 4 | 5 | 6 | 8 | 9 | … |
| y | … | 3.92 | 1.95 | 0.98 | 0.78 | 2.44 | 2.44 | 0.78 | … |
下面是小风的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=7对应的函数值y约为3.0.
②该函数的一条性质:该函数没有最大值.
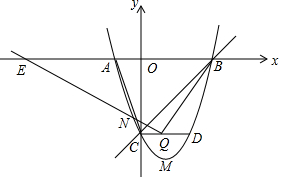 如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.
如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.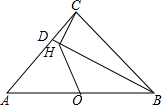 如图,△ABC中,∠ACB=90°,AC=BC=3,点D在AC上,CD=1,连接BD,过点C作CH⊥BD于点H,O为AB中点,连接OH,则OH的长为$\frac{3\sqrt{5}}{5}$.
如图,△ABC中,∠ACB=90°,AC=BC=3,点D在AC上,CD=1,连接BD,过点C作CH⊥BD于点H,O为AB中点,连接OH,则OH的长为$\frac{3\sqrt{5}}{5}$.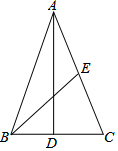 已知,如图△ABC中,AB=AC,AD⊥BC,BE是腰AC的中线,AD=12,BE=7.5,则△ABC的面积是36.
已知,如图△ABC中,AB=AC,AD⊥BC,BE是腰AC的中线,AD=12,BE=7.5,则△ABC的面积是36.