题目内容
3.某班课题学习小组对无盖的纸杯进行制作与探究,所要制作的纸杯如图1所示,规格要求是,杯口直径AB=6cm,杯底直径CD=4cm,杯壁母线AC=BD=6cm,请你和他们一起解决下列问题:(1)小颖同学先画出了纸杯的侧面展开示意图(如图2,忽略拼接部分),得到的图形是圆环的一部分.
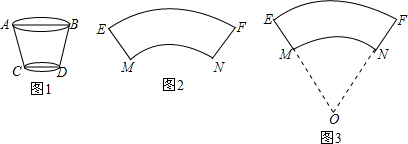
①图2中弧EF的长为6πcm,弧MN的4πcm,ME=NF=6cm;
②要想准确画出纸杯侧面的设计图,需要确定弧MN所在圆的圆心O,如图3所示,小颖同学发现若将弧EF、MN近似地看做线段,类比相似三角形的性质可得$\frac{弧EF的长}{弧MN的长}$=$\frac{OF}{ON}$,请你帮她证明这一结论.
③根据②中的结论,求弧MN所在圆的半径r及它所对的圆心角的度数n.
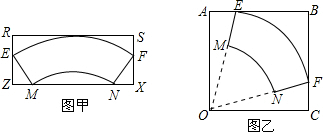
(2)小颖同学计划利用矩形,正方形纸各一张,分别按如图4和图5所示的方式剪出这个纸杯的侧面,求矩形纸片的长和宽以及正方形纸片的边长.
分析 (1)①根据圆的周长公式即可得出结论;
②设弧MN所在圆的半径为r,所对的圆心角度数为n,再根据弧长公式得出$\widehat{MN}$与$\widehat{EF}$的长,求出其比值即可;
③根据②中的结论求出r的值,再由①中两弧长即可得出n的值.
(2)延长EM交FN于点O,根据∠MON=60°得出△MON和△EOF是等边三角形,故可得出长方形的长,设RS与$\widehat{EF}$交于点P,OP交ZX于点Q,在Rt△OQN中,根据∠QON=30°,OQ=ON•cos30°,故可得出长方形的宽,设正方形边长为xcm,在Rt△BEF中根据勾股定理即可得出x的值.
解答 解:(1)①∵直径AB=6cm,杯底直径CD=4cm,杯壁母线AC=BD=6cm,
∴杯口圆的半径为3cm,杯底圆的半径为2cm,
∴$\widehat{EF}$的长=2×3π=6πcm,$\widehat{MN}$的长=2×2π=4πcm,ME=NF=AC=6cm.
故答案为:6π,4π,6;
②设弧MN所在圆的半径为r,所对的圆心角度数为n,则 $\widehat{MN}$的长度=$\frac{nπr}{180}$,$\widehat{EF}$ 的长=$\frac{nπ(r+FN)}{180}$,
所以$\frac{\widehat{EF}}{\widehat{MN}}$=$\frac{\frac{nπ(r+FN)}{180}}{\frac{nπr}{180}}$=$\frac{r+FN}{r}$=$\frac{ON+NF}{ON}$=$\frac{OF}{ON}$,
③由②得,$\frac{\widehat{EF}}{\widehat{MN}}$=$\frac{OF}{ON}$,即$\frac{6π}{4π}$=$\frac{r+6}{r}$,解得r=12,
∵$\widehat{MN}$的长=$\frac{nπr}{180}$,
∴$\frac{nπ×12}{180}$=4π,解得n=60,
即弧MN所在圆的半径r等于12cm,及它所对的圆心角的度数为60°;
(2)延长EM交FN于点O,
∵∠MON=60°,
∴△MON和△EOF是等边三角形,
∴EF=长方形的长=12+6=18,
设RS与$\widehat{EF}$ 交于点P,OP交ZX于点Q,连接OP,
∴OQ⊥MN,MQ=QN,
在Rt△OQN中,∠QON=30°,OQ=ON•cos30°=6$\sqrt{3}$,
∴长方形的宽=(18-6$\sqrt{3}$ )cm,
∵设正方形边长为xcm,
∴在Rt△AOE中,AO2+AE2=OE2,
∵OE=18,
∴BE=BF=9$\sqrt{2}$,
即x2+(x-9$\sqrt{2}$ )2=182,
化简得,x2-9$\sqrt{2}$ x-81=0,
解得x=$\frac{9}{2}$($\sqrt{2}$$±\sqrt{6}$),
∵x>0,
∴x=$\frac{9}{2}$($\sqrt{2}$+$\sqrt{6}$),
∴正方形边长为 $\frac{9}{2}$($\sqrt{2}$+$\sqrt{6}$)cm.
点评 本题考查的是圆的综合题,涉及到弧长的计算、勾股定理、锐角三角函数的定义等知识,难度适中,关键是理解题意,搞清楚弧长与底面圆的周长之间的关系是解题的关键.

| 气温(℃) | 20 | 21 | 22 | 23 | 24 |
| 天数(天) | 4 | 10 | 8 | 6 | 2 |
| A. | 21;21 | B. | 21;21.5 | C. | 21;22 | D. | 22;22 |
 如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.
如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.