已知x2+y2-8x-10y+41=0.求$\frac{x}{y}-\frac{y}{x}$的值．题目和参考答案——青夏教育精英家教网—

题目内容

4．已知x²+y²-8x-10y+41=0，求$\frac{x}{y}-\frac{y}{x}$的值．

分析直接利用完全平方公式将已知变形求出x，y的值，再代入原式求出答案．

解答解：∵x²+y²-8x-10y+41=0
∴（x-4）²+（y-5）²=0，
则x=4，y=5，
∴$\frac{x}{y}-\frac{y}{x}$=$\frac{4}{5}$-$\frac{5}{4}$=$\frac{16}{20}$-$\frac{25}{20}$=-$\frac{9}{20}$．

点评此题主要考查了完全平方公式的应用以及分式的化简求值，正确得出x，y的值是解题关键．

练习册系列答案

相关题目

14．用不等式表示“7与m的4倍的和是负数”就是7+4m＜0．

15．先化简，再求值：（x+2）²-（x+1）（x-1），其中x=2．

12．一辆汽车开往距离出发地180千米的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前40分钟到达目的地．设前一小时的速度为x千米/小时．则下列方程正确的是（　　）

	A．	$\frac{180}{x}$-40=$\frac{180-x}{1.5x}$		B．	$\frac{180}{x}$-40=1+$\frac{180-x}{1.5x}$
	C．	$\frac{180}{1.5x}$-$\frac{40}{60}$=1+$\frac{180-1.5x}{x}$		D．	$\frac{180}{x}$-$\frac{40}{60}$=1+$\frac{180-x}{1.5x}$

19．已知函数y=x+m²+m，当m==0或-1时，它是正比例函数．

9．若关于x的不等式组$\left\{\begin{array}{l}{x-a＜1}\\{x≥1}\end{array}\right.$的整数解有3个，则a的取值范围是（　　）

16．单项式8x^ay^b-1与2x^a+1y^b（a，b都是正整数）的公因式是2x^ay^b-1．

13．

如图，在Rt△ABC中，∠BAC=90°，D、E分别是AB、BC的中点，F在CA的延长线上，∠FDA=∠B，AC=6，AB=8，则四边形AEDF的周长为（　　）

14．

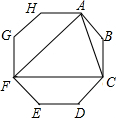连接正八边形的三个顶点，得到如图所示的图形，下列说法错误的是（　　）

	A．	△ACF是等边三角形
	B．	连接BF，则BF分别平分∠AFC和∠ABC
	C．	整个图形是轴对称图形，但不是中心对称图形
	D．	四边形AFGH与四边形CFED的面积相等

试题分类