题目内容
12.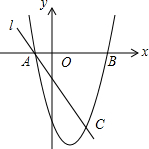 如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B、C三点的坐标;
(2)在抛物线的对称轴上找到点P,使得△PBC的周长最小,并求出点P的坐标;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G为顶点四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
分析 (1)因为抛物线与x轴相交,令y=0,解出A、B的坐标.再根据C点在抛物线上,C点的横坐标为2,代入抛物线中即可得出C点的坐标.
(2)根据两点式方程即可解出AC的函数表达式,根据轴对称-最短路径的确定顶点点P的位置,求出点P的坐标;
(3)存在四个这样的点.①连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(-3,0);
②AF=CG=2,A点的坐标为(-1,0),因此F点的坐标为(1,0);
③此时C,G两点的纵坐标关于x轴对称,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+$\sqrt{7}$,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=-x+h,将G点代入后可得出直线的解析式为y=-x+7.因此直线GF与x轴的交点F的坐标为(4+$\sqrt{7}$,0);
④如图,同③可求出F的坐标为(4-$\sqrt{7}$,0);综合四种情况可得出,存在4个符合条件的F点.
解答  解:(1)令y=0,则x2-2x-3=0,
解:(1)令y=0,则x2-2x-3=0,
解得x1=-1,x2=3,
∴A(-1,0)B(3,0),
将C点的横坐标x=2代入y=x2-2x-3,得y=-3,
∴C(2,-3);
(2)设直线AC的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=-3}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
∴直线AC的函数解析式是y=-x-1,
由抛物线的对称性可知,点A与点B关于对称轴x=1对称,
∴连接AC与x=1交于点P,点即为所求,
当x=1时,y=-2,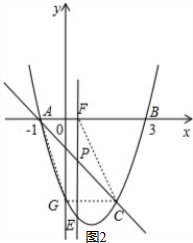
则点P的坐标为(1,-2);
(3)存在4个这样的点F,
①如图1,连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(-3,0);
②如图2,AF=CG=2,A点的坐标为(-1,0),因此F点的坐标为(1,0);
③如图3,此时C,G两点的纵坐标互为相反数,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+$\sqrt{7}$,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=-x+h,将G点代入后可得出直线的解析式为y=-x+4+$\sqrt{7}$.因此直线GF与x轴的交点F的坐标为(4+$\sqrt{7}$,0);
④如图4,同③可求出F的坐标为(4-$\sqrt{7}$,0),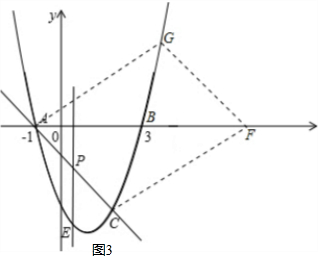
综合四种情况可得出,存在4个符合条件的F点.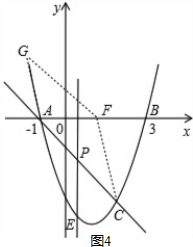
点评 本题着重考查了待定系数法求一次函数解析式、平行四边形的判定、二次函数的性质、轴对称-最短路径问题等重要知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

 名校课堂系列答案
名校课堂系列答案| A. | $\left\{\begin{array}{l}{k=2}\\{m=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{k=2}\\{m=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{k=3}\\{m=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{k=-3}\\{m=-2}\end{array}\right.$ |
| A. | 代入法 | |
| B. | 加减法 | |
| C. | 消元,化二元为一元 | |
| D. | 由一个未知数的值求另一个未知数的值 |
| A. | 只有①是对的 | B. | 只有②是对的 | C. | ①②都是对的 | D. | ①②都是错的 |