题目内容
16.已知:点A(x1,y1)、B(x2,y2)、C(x3,y3)是函数y=-$\frac{3}{x}$图象上的三点,且x1<0<x2<x3,则y1、y2、y3的大小关系是y2<y3<y1.分析 先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再由x1<0<x2<x3判断出各点所在的象限,进而可得出结论.
解答 解:∵函数y=-$\frac{3}{x}$中,k=-3<0,
∴此函数的图象的两个分支位于二四象限,且在每一象限内,y随x的增大而增大.
∵x1<0<x2<x3,
∴点A(x1,y1)在第二象限,B(x2,y2)、C(x3,y3)在第四象限,
∴y1>0,y2<y3<0,
∴y2<y3<y1.
故答案为:y2<y3<y1.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
4.若|x|=|y|,那么x与y之间的关系是( )
| A. | 相等 | B. | 互为相反数 | ||
| C. | 相等或互为相反数 | D. | 无法判断 |
 如图,⊙O的直径CD⊥AB,∠AOC=60°,则∠CDB=30°.
如图,⊙O的直径CD⊥AB,∠AOC=60°,则∠CDB=30°.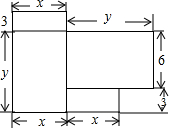 小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).
小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m). 如图所示,△ABC是等边三角形,D是AC的中点,延长BC到E,使CE=$\frac{1}{2}$BC,等于30°的角有4个.
如图所示,△ABC是等边三角形,D是AC的中点,延长BC到E,使CE=$\frac{1}{2}$BC,等于30°的角有4个.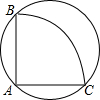 如图有一个直径为8的圆形铁皮,要从中剪出一个圆心角为90°的最大扇形ABC,用此剪下的扇形铁皮围成一个圆锥的侧面,则此圆锥的高为$\sqrt{30}$(结果保留根号).
如图有一个直径为8的圆形铁皮,要从中剪出一个圆心角为90°的最大扇形ABC,用此剪下的扇形铁皮围成一个圆锥的侧面,则此圆锥的高为$\sqrt{30}$(结果保留根号).