题目内容
12.半径为4的圆中,垂直平分一条半径的弦的长是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 首先作出图形,连接OA,在直角△OAD中根据勾股定理即可求得AD的长,则弦AB=2AD.
解答  解:如图所示,
解:如图所示,
连接OA,在直角△OAD中,
∵OA=4cm,OD=2cm,
∴AD=$\sqrt{{OA}^{2}-{OD}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴AB=2AD=4$\sqrt{3}$.
故选D.
点评 本题考查的是垂径定理,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
6.下列各组数中,数值相等的是( )
| A. | 23和32 | B. | -53和(-5)3 | C. | (-$\frac{2}{3}$)2和(-$\frac{3}{2}$)2 | D. | (-3)4和(-4)3 |
17. 如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
 如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )| A. | 47° | B. | 46° | C. | 45° | D. | 44° |
4.若|x|=|y|,那么x与y之间的关系是( )
| A. | 相等 | B. | 互为相反数 | ||
| C. | 相等或互为相反数 | D. | 无法判断 |
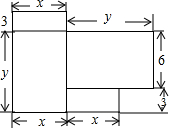 小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).
小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).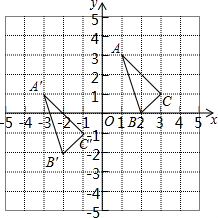 △ABC与△A′B′C′在平面直角坐标系中的位置如图.
△ABC与△A′B′C′在平面直角坐标系中的位置如图.