题目内容
一次函数y=kx+b的图象经过点P(0,-2),且与两坐标轴围成的三角形面积为3,求k、b的值.
考点:一次函数图象上点的坐标特征
专题:计算题
分析:先把P点坐标代入y=kx+b可计算出b的值,再用k表示一次函数与x轴的交点坐标,然后根据三角形面积公式得到
×2×|
|=3,再解方程即可得到k的值.
| 1 |
| 2 |
| 2 |
| k |
解答:解:把P(0,-2)代入y=kx+b得b=-2,
把y=0代入y=kx-2得kx-2=0,解得x=
,则一次函数图象与x轴的交点坐标为(
,0),
因为一次函数y=kx+b的图象与两坐标轴围成的三角形面积为3,
所以
×2×|
|=3,解得k=±
,
即k的值为±
,b的值为-2.
把y=0代入y=kx-2得kx-2=0,解得x=
| 2 |
| k |
| 2 |
| k |
因为一次函数y=kx+b的图象与两坐标轴围成的三角形面积为3,
所以
| 1 |
| 2 |
| 2 |
| k |
| 2 |
| 3 |
即k的值为±
| 2 |
| 3 |
点评:本题考查了一次函数图形上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b);直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
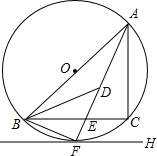 如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.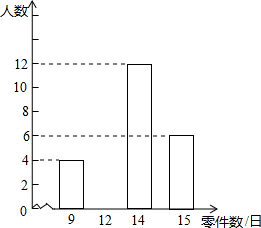 某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题: 如图,△ABD、△BCE、△ACF均为等边三角形,请回答下列问题(不要求证明)
如图,△ABD、△BCE、△ACF均为等边三角形,请回答下列问题(不要求证明)