题目内容
 如图,在△ABC中,AB=BC=AC=BF,∠BAC=∠ABC=∠ACB,BD=DA,∠1=∠2,求∠BFD的度数.
如图,在△ABC中,AB=BC=AC=BF,∠BAC=∠ABC=∠ACB,BD=DA,∠1=∠2,求∠BFD的度数.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:连接AD,首先证明△ADC≌△BDC可得∠ACD=∠BCD=30°,再证明△BFD≌△BCD可得∠BFD=∠BCD=30°.
解答: 解:连接AD,
解:连接AD,
∵在△ADC和△BDC中
,
∴△ADC≌△BDC(SSS),
∴∠ACD=∠BCD,
∵∠BAC=∠ABC=∠ACB,
∴∠ACB=60°,
∴∠BCD=30°,
在△BDF和△BDC中
,
∴△BFD≌△BCD(SAS),
∴∠BFD=∠BCD=30°.
 解:连接AD,
解:连接AD,∵在△ADC和△BDC中
|
∴△ADC≌△BDC(SSS),
∴∠ACD=∠BCD,
∵∠BAC=∠ABC=∠ACB,
∴∠ACB=60°,
∴∠BCD=30°,
在△BDF和△BDC中
|
∴△BFD≌△BCD(SAS),
∴∠BFD=∠BCD=30°.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形对应角相等.

练习册系列答案
相关题目
 如图,在方格纸中选择标有序号①②③④的一个小正方形涂黑,使它与图中阴影部分组成的新图形为中心对称图形,该小正方形的序号是( )
如图,在方格纸中选择标有序号①②③④的一个小正方形涂黑,使它与图中阴影部分组成的新图形为中心对称图形,该小正方形的序号是( ) 如图,PA、PB切⊙O于点A、B,PA=6,∠APB=60°,求阴影部分周长和面积.
如图,PA、PB切⊙O于点A、B,PA=6,∠APB=60°,求阴影部分周长和面积.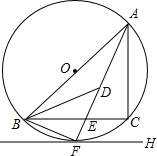 如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF. 已知:如图,△ABC≌△CAD.
已知:如图,△ABC≌△CAD. 一个正方形和两个等边三角形的位置如图,若∠3=50°,则∠1+∠2=
一个正方形和两个等边三角形的位置如图,若∠3=50°,则∠1+∠2=