题目内容
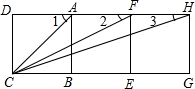 如图所示,三个边长为1个单位长度的正方形ABCD、ABEF、EFHG拼在一起.
如图所示,三个边长为1个单位长度的正方形ABCD、ABEF、EFHG拼在一起.(1)计算:AC边的长度;
(2)△ACF与△AHC相似吗?说明你的理由;
(3)直接写出∠1,∠2,∠3间的数量关系.
考点:相似三角形的判定与性质,正方形的性质
专题:计算题
分析:(1)利用勾股定理计算出AC的长;
(2)先分别得到AC=
,AF=1,AH=2,则
=
=
,加上公共角,于是可判断△ACF∽△AHC;
(3)由△ACF∽△AHC得到∠2=∠ACH,然后利用三角形外角性质可得∠1=∠ACH+∠3=∠2+∠3.
(2)先分别得到AC=
| 2 |
| AH |
| AC |
| AC |
| AF |
| 2 |
(3)由△ACF∽△AHC得到∠2=∠ACH,然后利用三角形外角性质可得∠1=∠ACH+∠3=∠2+∠3.
解答:解:(1)AC=
=
;
(2)△ACF∽△AHC.理由如下:
∵AC=
,AF=1,AH=2,
∴
=
=
,
而∠FAC=∠CAH,
∴△ACF∽△AHC;
(3)∵△ACF∽△AHC
∴∠2=∠ACH,
而∠1=∠ACH+∠3,
∴∠1=∠2+∠3.
| 12+12 |
| 2 |
(2)△ACF∽△AHC.理由如下:
∵AC=
| 2 |
∴
| AH |
| AC |
| AC |
| AF |
| 2 |
而∠FAC=∠CAH,
∴△ACF∽△AHC;
(3)∵△ACF∽△AHC
∴∠2=∠ACH,
而∠1=∠ACH+∠3,
∴∠1=∠2+∠3.
点评:本题考查了相似三角形的判定与性质:三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,判定三角形相似的方法有事可单独使用,有时需要综合运用,无论是单独使用还是综合运用,都要具备应有的条件方可.也考查了正方形的性质.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
把27430用科学记数法表示应是( )
| A、0.2743×103 |
| B、27.43×103 |
| C、274.3×10 |
| D、2.743×104 |
 如图,如果∠AON=∠BOM,OC平分∠MON,那么图中除∠AON=∠BOM外,相等的角还有( )
如图,如果∠AON=∠BOM,OC平分∠MON,那么图中除∠AON=∠BOM外,相等的角还有( )| A、1对 | B、2对 | C、3对 | D、4对 |
 在直角Rt△ABC中,∠C=90°,∠B=15°,BC=2+
在直角Rt△ABC中,∠C=90°,∠B=15°,BC=2+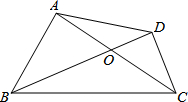 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.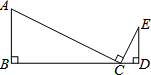 如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE.AB=3,DE=2,BC=6.求CD的长.
如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE.AB=3,DE=2,BC=6.求CD的长.
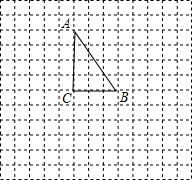 如图,△ABC的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度.
如图,△ABC的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度.