题目内容
16. 如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:等边三角形;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论.
分析 (1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
(2)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得.
解答 解:(1)△ABC是等边三角形.
证明如下:在⊙O中
∵∠BAC与∠CPB是$\widehat{BC}$所对的圆周角,∠ABC与∠APC是$\widehat{AC}$所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:等边三角形;
(2)在PC上截取PD=AP,如图,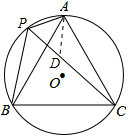
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
$\left\{\begin{array}{l}{∠APB=∠ADC}\\{∠ABP=∠ACD}\\{AP=AD}\end{array}\right.$,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.
点评 本题考查了圆周角定理、等边三角形的判定、以及三角形的全等的判定与性质,正确作出辅助线,证明△APB≌△ADC是关键.

练习册系列答案
相关题目
19.计算(a-$\frac{b^2}{a}$)•$\frac{a}{a-b}$的结果是( )
| A. | $\frac{1}{a-b}$ | B. | $\frac{1}{a+b}$ | C. | a-b | D. | a+b |
4. 如图,在∠1、∠2、∠3、∠4中,内错角是( )
如图,在∠1、∠2、∠3、∠4中,内错角是( )
 如图,在∠1、∠2、∠3、∠4中,内错角是( )
如图,在∠1、∠2、∠3、∠4中,内错角是( )| A. | ∠1与∠4 | B. | ∠2与∠4 | C. | ∠1与∠3 | D. | ∠2与∠3 |
6.下列两个三角形不一定相似的是( )
| A. | 两个等边三角形 | B. | 两个全等三角形 | ||
| C. | 两个等腰直角三角形 | D. | 有一个30°角的两个等腰三角形 |
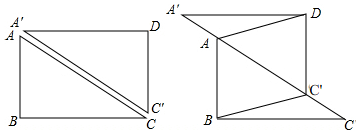
 将一副直角三角尺BAC和ADE如图放置,其中∠BCA=30°,∠AED=45°,若∠AFD=75°,试判断AE与BC的位置关系,并说明理由.
将一副直角三角尺BAC和ADE如图放置,其中∠BCA=30°,∠AED=45°,若∠AFD=75°,试判断AE与BC的位置关系,并说明理由. 如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.
如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长. 如图,点D、E在BC上,AB=AC,AD=AE.∠BAD和∠CAE有怎样的关系?请说明理由.
如图,点D、E在BC上,AB=AC,AD=AE.∠BAD和∠CAE有怎样的关系?请说明理由.