题目内容
2．
如图，在3×3的正方形网格中标出了∠1和∠2，则∠1+∠2=45°．
分析 根据网格结构以∠1的顶点为顶点作出与∠2所在的直角三角形全等的三角形，再连接另两个顶点得到等腰直角三角形，然后根据等腰直角三角形的性质解答．
解答 
解：如图，∠2、∠3为两个全等三角形的对应角，
所以，∠2=∠3，
△ABC是等腰直角三角形，
所以，∠1+∠3=45°，
所以，∠1+∠2=45°．
故答案为：45．
点评 本题考查了全等三角形，熟练掌握网格结构，作出与∠2所在的直角三角形全等的三角形是解题的关键．
练习册系列答案
相关题目
1．
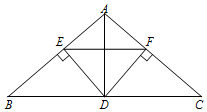如图，在△ABC中，AB=AC，D是边BC上一点，DE⊥AB，DF⊥AC，垂足分别是E、F，△AEF∽△ABC．
（1）求证：△AED≌△AFD；
（2）若BC=2AD，求证：四边形AEDF是正方形．
如图，在△ABC中，AB=AC，D是边BC上一点，DE⊥AB，DF⊥AC，垂足分别是E、F，△AEF∽△ABC．（1）求证：△AED≌△AFD；
（2）若BC=2AD，求证：四边形AEDF是正方形．
如图，圆柱体的高为4cm，底面周长为6cm，小蚂蚁在圆柱表面爬行，从A点到B点，路线如图所示，则最短路程为5cm．
7．
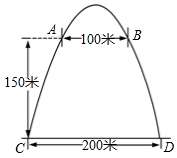如图，拱门的地面宽度为200米，两侧距地面高150米处各有一个观光窗，两窗的水平距离为100米，则拱门的最大高度（ ）
如图，拱门的地面宽度为200米，两侧距地面高150米处各有一个观光窗，两窗的水平距离为100米，则拱门的最大高度（ ）| A． | 100米 | B． | 150米 | C． | 200米 | D． | 300米 |
14．
如图是一个三角形的算法图，每个方框里有一个数，这个数等于它所在边的两个圆圈里的数的和，则图中①②③三个圆圈里的数依次是（ ）
如图是一个三角形的算法图，每个方框里有一个数，这个数等于它所在边的两个圆圈里的数的和，则图中①②③三个圆圈里的数依次是（ ）| A． | 19，7，14 | B． | 11，20，19 | C． | 14，7，19 | D． | 7，14，19 |
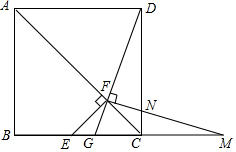如图．在正方形ABCD中，点E是BC边上的中点，EF⊥AC于点F．连接DF并延长交BC于G．过F作FM⊥DG交CD于N，交BC的延长线于点M．