题目内容
11．对于任意有理数a、b、c、d，我们规定符号（a，b）?（c，d）=ad-bc，例如：（1，3）?（2，4）=1×4-2×3=-2．
（1）求（-2，3）?（4，5）的值为-22；
（2）求（3a+1，a-2）?（a+2，a-3）的值，其中a2-4a+1=0．
分析 （1）利用新定义得到（-2，3）?（4，5）=-2×5-3×4，然后进行有理数的混合运算即可；
（2）利用新定义得到原式=（3a+1）（a-3）-（a-2）（a+2），然后去括号后合并，最后利用整体代入的方法计算．
解答 解：（1）（-2，3）?（4，5）=-2×5-3×4=-10-12=-22；
故答案为-22；
（2）（3a+1，a-2）?（a+2，a-3）=（3a+1）（a-3）-（a-2）（a+2）
=3a2-9a+a-3-（a2-4）
=3a2-9a+a-3-a2+4
=2a2-8a+1，
∵a2-4a+1=0，
∴a2=4a-1，
∴3a+1，a-2）?（a+2，a-3）=2（4a-1）-8a+1=-1．
点评 本题考查了整式的混合运算-化简求值：先按运算顺序把整式化简，再把对应字母的值代入求整式的值．有乘方、乘除的混合运算中，要按照先乘方后乘除的顺序运算，其运算顺序和有理数的混合运算顺序相似．
练习册系列答案
相关题目
如图，在3×3的正方形网格中标出了∠1和∠2，则∠1+∠2=45°．
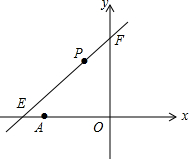如图，直线l：y=kx+6与x轴、y轴分别相交于E、F，点E的坐标为（-9，0），点A的坐标为（-6，0），点P（x，y）是直线l上的一个动点．
