题目内容
 如图,⊙O是△ABC的外接圆,若∠B=30°,AC=
如图,⊙O是△ABC的外接圆,若∠B=30°,AC=| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:三角形的外接圆与外心
专题:计算题
分析:作直径AD,连结CD,如图,根据圆周角定理得到∠ACD=90°,∠D=∠B=30°,然后根据含30度的直角三角形三边的关系即可得到AD=2AC=2
.
| 3 |
解答:解: 作直径AD,连结CD,如图,
作直径AD,连结CD,如图,
∵AD为直径,
∴∠ACD=90°,
∵∠D=∠B=30°,
∴AD=2AC=2
.
故选D.
 作直径AD,连结CD,如图,
作直径AD,连结CD,如图,∵AD为直径,
∴∠ACD=90°,
∵∠D=∠B=30°,
∴AD=2AC=2
| 3 |
故选D.
点评:本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理.

练习册系列答案
相关题目
 如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )
如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )A、
| ||
| B、11cm | ||
| C、13cm | ||
| D、17cm |
 如图,在正八边形ABCDEFGH中,若四边形BCFG的面积是12cm2,则正八边形的面积为
如图,在正八边形ABCDEFGH中,若四边形BCFG的面积是12cm2,则正八边形的面积为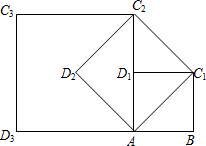 如图,在正方形ABC1D1中,AB=1.连接AC1,以AC1为边作第二个正方形AC1C2D2;连接AC2,以AC2为边作第三个正方形AC2C3D3.则
如图,在正方形ABC1D1中,AB=1.连接AC1,以AC1为边作第二个正方形AC1C2D2;连接AC2,以AC2为边作第三个正方形AC2C3D3.则 如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为
如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为