题目内容
18.先化简,再求值:$\frac{x}{{x}^{2}-1}$+($\frac{x+1}{x-1}$-$\frac{x-1}{{x}^{2}-2x+1}$),然后-$\sqrt{7}$≤x≤$\sqrt{7}$的范围内选取一个合适的整数作为x的值代入求值.分析 先进行括号里面的减法运算,再进行加法运算求得结果,最后选择合适的x的值,代入所得结果计算求值.
解答 解:原式=$\frac{x}{(x+1)(x-1)}$+[$\frac{x+1}{x-1}$-$\frac{x-1}{(x-1)^{2}}$]
=$\frac{x}{(x+1)(x-1)}$+($\frac{x+1}{x-1}$-$\frac{1}{x-1}$)
=$\frac{x}{(x+1)(x-1)}$+$\frac{x}{x-1}$
=$\frac{x}{(x+1)(x-1)}$+$\frac{{x}^{2}+x}{(x+1)(x-1)}$
=$\frac{{x}^{2}+2x}{(x+1)(x-1)}$
=$\frac{{x}^{2}+2x}{{x}^{2}-1}$
∵-$\sqrt{7}$≤x≤$\sqrt{7}$,且x为整数
∴要使分式有意义,则x能取0、2或-2
∴当x=-2时,原式=$\frac{4-4}{4-1}$=0,
或当x=2时,原式=$\frac{4+4}{4-1}$=$\frac{8}{3}$,
或当x=0时,原式=$\frac{0}{-1}$=0.
点评 本题主要考查了分式的化简求值,解决问题的关键是掌握分式的通分与约分.通分时要注意:若各分式的分母能分解因式,一定要先分解因式,然后再去找各分母的最简公分母.在求值时要注意:所取的x的值不能使原分式无意义.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
9.一种细菌的半径为6.5×10-5米,该数字用小数可表示为( )
| A. | 0.0065 | B. | 0.00065 | C. | 0.000065 | D. | 0.0000065 |
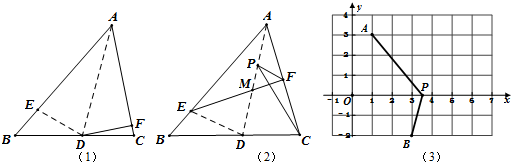
 如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为6$\sqrt{2}$.
如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为6$\sqrt{2}$.