题目内容
某广告公司设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
考点:二次函数的应用
专题:
分析:(1)根据矩形周长为12m,一边长为x,得出另一边为6-x,再根据矩形的面积公式即可得出答案.
(2)根据(1)得出的关系式,利用配方法进行整理,可求出函数的最大值,从而得出答案.
(2)根据(1)得出的关系式,利用配方法进行整理,可求出函数的最大值,从而得出答案.
解答:解:(1)∵矩形的一边长为x米,
∴另一边长为
米,即(6-x)米,
∴S=x(6-x)=-x2+6x,
即S=-x2+6x,其中0<x<6;
(2)根据(1)得:S=x(6-x)=-(x-3)2+9,
则矩形一边长为3m时,面积最大为9m2,
则此时最大费用为9×1000=9000(元).
∴另一边长为
| 12-2x |
| 2 |
∴S=x(6-x)=-x2+6x,
即S=-x2+6x,其中0<x<6;
(2)根据(1)得:S=x(6-x)=-(x-3)2+9,
则矩形一边长为3m时,面积最大为9m2,
则此时最大费用为9×1000=9000(元).
点评:本题考查的是二次函数的实际应用以及矩形面积的计算公式,关键是根据矩形的面积公式=长×宽列出关系式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
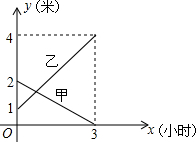 某企业有甲乙两个长方形的蓄水池,将甲池中的水注入乙池,甲乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数图象如图,结合图象回答下列问题:
某企业有甲乙两个长方形的蓄水池,将甲池中的水注入乙池,甲乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数图象如图,结合图象回答下列问题: