Question

6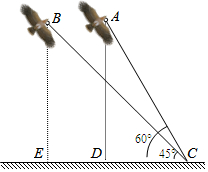．在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C处（如图）．现已知风筝A的引线（线段AC）长20m，风筝B的引线（线段BC）长24m，在C处测得风筝A的仰角为60°，风筝B的仰角为45°．
（1）试通过计算，比较风筝A与风筝B谁离地面更高？
（2）求风筝A与风筝B的水平距离．（精确到0.01m）
sin45°≈0.707，cos45°≈0.707，tan45°=1，sin60°≈0.866，cos60°=0.5，tan60°≈1.732．

Answer 1

分析 （1）在直角三角形中，运用三角函数定义求解；
（2）利用已知角的余弦函数求CE，CD．距离=CE-CD．

解答 解：（1）分别过A，B作地面的垂线，垂足分别为D，E．
在Rt△ADC中，
∵AC﹦20，∠ACD﹦60°，
∴AD﹦20×sin60°﹦10$\sqrt{3}$≈17.32．
在Rt△BEC中，
∵BC﹦24，∠BCE﹦45°，
∴BE﹦24×sin45°﹦12$\sqrt{3}$≈16.97．
∵17.32＞16.97，
∴风筝A比风筝B离地面更高．                     

（2）在Rt△ADC中，
∵AC﹦20，∠ACD﹦60°，
∴DC﹦20×cos60°﹦10．
在Rt△BEC中，
∵BC﹦24，∠BEC﹦90°，
∴EC=BC×cos45°≈24×0.707≈16.97（m），
∴EC-DC≈16.97-10﹦6.97（m）．
即风筝A与风筝B的水平距离约为6.97m．

点评 本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．