题目内容
20.满足下列条件的△ABC,不是直角三角形的是( )| A. | BC=1,AC=2,AB=$\sqrt{3}$ | B. | BC:AC:AB=12:13:5 | ||
| C. | ∠A+∠B=∠C | D. | ∠A:∠B:∠C=3:4:5 |
分析 根据勾股定理的逆定理可判定A、B,由三角形内角和可判定C、D,可得出答案.
解答 解:A、当BC=1,AC=2,AB=$\sqrt{3}$时,满足BC2+AB2=1+3=4=AC2,所以△ABC为直角三角形;
B、当BC:AC:AB=12:13:5时,设BC=12x,AC=13x,AB=5x,
满足BC2+AB2=AC2,
所以△ABC为直角三角形;
C、当∠A+∠B=∠C时,且∠A+∠B+∠C=180°,所以∠C=90°,所以△ABC为直角三角形;
D、当∠A:∠B:∠C=3:4:5时,可设∠A=3x°,∠B=4x°,∠C=5x°,
由三角形内角和定理可得3x+4x+5x=180,解得x=15°,
所以∠A=45°,∠B=60°,∠C=75°,
所以△ABC为锐角三角形.
故选D.
点评 本题主要考查直角三角形的判定方法,掌握直角三角形的判定方法是解题的关键,主要有①勾股定理的逆定理,②有一个角为直角的三角形.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
10.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (2a+1)(2a-1)=4a-1 | C. | (-2a3)2=4a6 | D. | x2-8x+16=(x+4)2 |
11.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为( )
| A. | 7sin35° | B. | 7cos35° | C. | 7tan35° | D. | $\frac{7}{cos35°}$ |
15.下列方程中两个实数根的和等于2的方程是( )
| A. | 2x2-4x+3=0 | B. | 2x2-2x-3=0 | C. | 2y2+4y-3=0 | D. | 2t2-4t-3=0 |
5. 一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时候到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时候到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
 一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时候到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时候到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )| A. | 80海里 | B. | 70海里 | C. | 60海里 | D. | 40海里 |
12.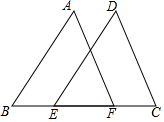 如图,点E,F在BC上,BE=CF,∠B=∠C,若要证明△ABF≌△DCE,则还需要补充的条件不可能是( )
如图,点E,F在BC上,BE=CF,∠B=∠C,若要证明△ABF≌△DCE,则还需要补充的条件不可能是( )
 如图,点E,F在BC上,BE=CF,∠B=∠C,若要证明△ABF≌△DCE,则还需要补充的条件不可能是( )
如图,点E,F在BC上,BE=CF,∠B=∠C,若要证明△ABF≌△DCE,则还需要补充的条件不可能是( )| A. | ∠A=∠D | B. | ∠AFB=∠DEC | C. | AF=DE | D. | AB=CD |
9.下列各组数:①-1与+1;②+(+1)与-1;③-(-2)与+(-2);④-(-$\frac{1}{2}$)与+(+$\frac{1}{2}$):⑤+[-(+1)]与-[+(-1)];⑥-(+2)与-(-2),其中,互为相反数的有( )
| A. | 6组 | B. | 5组 | C. | 4组 | D. | 3组 |
10. 如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
 如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )| A. | 6$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 9 | D. | 4.5 |
 如图,AB∥DG,∠1+∠2=180°,
如图,AB∥DG,∠1+∠2=180°,