题目内容
10. 如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )| A. | 6$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 9 | D. | 4.5 |
分析 连接BD,得出△ABD是等边三角形,由于菱形的对角线互相垂直平分,所以PD=BP,连接MD,由等边三角形的性质可知DM⊥AB,再根据∠ADM=30°即可求出AB的长.
解答 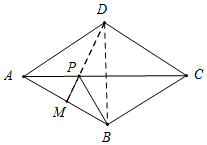 解:如图所示,连接DP,则根据菱形的对角线互相垂直平分,可得PD=BP,
解:如图所示,连接DP,则根据菱形的对角线互相垂直平分,可得PD=BP,
当点M,P,D三点共线时,BP+MP=DP+MP=DM=9(最短),
连接BD,根据∠BAD=60°,可得△ABD是等边三角形,
∵点M是AB的中点,
∴DM⊥AB,
∴∠ADM=30°,
∵AM=$\frac{DM}{\sqrt{3}}$=3$\sqrt{3}$,
∴AD=2AM=6$\sqrt{3}$,
∴AB=6$\sqrt{3}$,
故选:A.
点评 本题是最短线路问题,考查的是菱形的性质以及等边三角形的性质在综合应用,由菱形的性质得出点D是点B关于AC的对称点是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.满足下列条件的△ABC,不是直角三角形的是( )
| A. | BC=1,AC=2,AB=$\sqrt{3}$ | B. | BC:AC:AB=12:13:5 | ||
| C. | ∠A+∠B=∠C | D. | ∠A:∠B:∠C=3:4:5 |
5.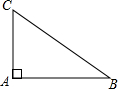 如图,在△ABC中,∠A=90°,若AB=8,AC=6,则cosC的值为( )
如图,在△ABC中,∠A=90°,若AB=8,AC=6,则cosC的值为( )
 如图,在△ABC中,∠A=90°,若AB=8,AC=6,则cosC的值为( )
如图,在△ABC中,∠A=90°,若AB=8,AC=6,则cosC的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
15. 如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
 如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
2.下列每组数分别是三根木棒的长度,不折断且将它们收尾相连时,能摆成三角形的是( )
| A. | 3cm,4cm,8cm | B. | 8cm,7cm,15cm | C. | 5cm,5cm,11cm | D. | 13cm,12cm,20cm |
19.小颖把积蓄的a元零花钱存入银行,存了3年,年利率是b,到期后小颖可以取出的本息和为( )
| A. | a+3ab | B. | a(1+b)3 | C. | a+3(1+b) | D. | 3ab |
20.下列图象不能表示y是x的函数图象的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.
如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.