题目内容
12．
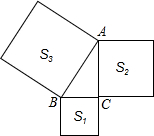如图，在直角三角形ABC的三边上，向外做三个正方形，其中两个的面积为S3=110，S2=60，则另一个正方形的边长BC为5$\sqrt{2}$．
分析 根据正方形的面积公式，运用勾股定理可以证明S1+S2=S3，进而可得出结论．
解答 解：∵∠ACB=90°，
∴BC2+AC2=AB2，
∵S1=BC2，S2=AC2，S3=AB2，
∴S1+S2=S3，
∴S1=100-60=50，
∴BC=5$\sqrt{2}$．
故答案为：5$\sqrt{2}$．
点评 本题考查勾股定理，正方形面积公式，解题的关键是证明S1+S2=S3，记住这个结论在以后解题中会有帮助，属于基础题中考常考题型．
练习册系列答案
相关题目
2．下列运算正确的是（ ）
| A． | a2•a3=a6 | B． | （a3）2=a9 | C． | a4+b4=（a+b）4 | D． | （a6）2÷（a4）3=1 |
20．在-1.414，$\frac{22}{7}$，$\root{3}{-27}$，$\frac{π}{3}$，-$\sqrt{2}$，3.14，$\sqrt{9}$，0.1212212221…（两个1之间依次多1个2）中，无理数的个数是（ ）
| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
17．下列代数式变形正确的是（ ）
| A． | -a+b=（a+b） | B． | -4a2+b2=（2a-b）（2a+b） | ||
| C． | （-x-y）2=（x+y）2 | D． | x2-4x-3=（x-2）2-3 |
4．把$\frac{{-\sqrt{45{y^2}}}}{{3\sqrt{5y}}}$化简后得（ ）
| A． | $\frac{{-\sqrt{9y}}}{3}$ | B． | $-\sqrt{y}$ | C． | $-3\sqrt{5y}$ | D． | $\frac{{3\sqrt{5}}}{5}$ |