题目内容
20.在△ABC中,AD平分∠BAC,∠ACB>∠B.求证:∠ADC=90°-$\frac{1}{2}$(∠ACB-∠B)分析 根据题意画出图形,再由角平分线的性质及三角形内角和定理即可得出结论.
解答  证明:如图,∵AD平分∠BAC,
证明:如图,∵AD平分∠BAC,
∴∠BAD=∠DAC=$\frac{1}{2}$∠BAC.
∵∠ADC=180°-∠ADB
=∠B+∠BAD
=∠B+$\frac{1}{2}$∠BAC
=∠B+$\frac{1}{2}$(180°-∠ACB-∠B)
=90°-$\frac{1}{2}$∠ACB+∠B
=90°-$\frac{1}{2}$(∠ACB-∠B)
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
15.一定是全等三角形的是( )
| A. | 面积相等的三角形 | B. | 周长相等的三角形 | ||
| C. | 形状相同的三角形 | D. | 能够完全重合的两个三角形 |
12.在△ABC中,AB=15,BC=12,AC=9,则△ABC的面积为( )
| A. | 180 | B. | 90 | C. | 54 | D. | 108 |
 如图,点D、E分别为△ABC的边AB、AC的中点,同时,点F在DE上,且∠AFB=90°,已知AB=5,BC=8,那么EF的长为1.5.
如图,点D、E分别为△ABC的边AB、AC的中点,同时,点F在DE上,且∠AFB=90°,已知AB=5,BC=8,那么EF的长为1.5.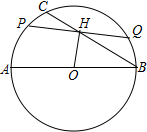 在⊙O中,直径AB=8,∠ABC=30°,点H在弦BC上,弦PQ⊥OH于点H.当点P在$\widehat{AC}$上移动时,PQ长的最大值为4$\sqrt{3}$.
在⊙O中,直径AB=8,∠ABC=30°,点H在弦BC上,弦PQ⊥OH于点H.当点P在$\widehat{AC}$上移动时,PQ长的最大值为4$\sqrt{3}$.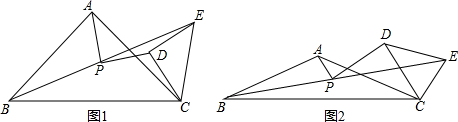
 在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图?、图②、…,则旋转得到的图
在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图?、图②、…,则旋转得到的图 的直角顶点的坐标为(8064,0).
的直角顶点的坐标为(8064,0).