题目内容
10. 在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图?、图②、…,则旋转得到的图
在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图?、图②、…,则旋转得到的图 的直角顶点的坐标为(8064,0).
的直角顶点的坐标为(8064,0).
分析 利用勾股定理得到AB的长度,结合图形可求出图③的直角顶点的坐标;根据图形不难发现,每3个图形为一个循环组依次循环,且下一组的第一个图形与上一组的最后一个图形的直角顶点重合.
解答 解:∵∠AOB=90°,OA=3,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴旋转得到图③的直角顶点的坐标为(12,0);
根据图形,每3个图形为一个循环组,3+5+4=12,
因为2015÷3=671…2
所以, 的直角顶点在x轴上,横坐标为671×12+3+5=8064,
的直角顶点在x轴上,横坐标为671×12+3+5=8064,
所以,图 的顶点坐标为(8064,0),
的顶点坐标为(8064,0),
故答案是:(8064,0).
点评 本题考查了坐标与图形的变化-旋转,仔细观图形,判断出旋转规律“每3个图形为一个循环组依次循环,且下一组的第一个图形与上一组的最后一个图形的直角顶点重合”是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 尺规作图:(要求保留作图痕迹)
尺规作图:(要求保留作图痕迹) 在数轴上表示下列各数,并用“>”连接.
在数轴上表示下列各数,并用“>”连接.
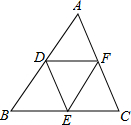 如图,点D,E,F分别是△ABC的AB,BC,CA边的中点.若△DEF的周长为10,则△ABC的周长为20.
如图,点D,E,F分别是△ABC的AB,BC,CA边的中点.若△DEF的周长为10,则△ABC的周长为20.