题目内容
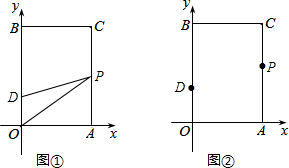
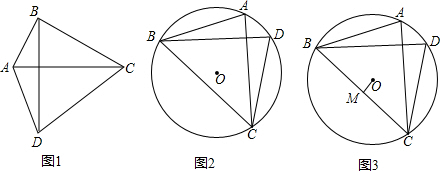
19.已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为$\frac{ab}{a+b}$的是( )| A. | 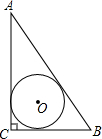 | B. | 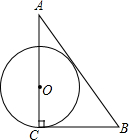 | C. | 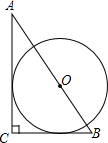 | D. | 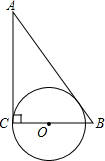 |
分析 利用圆与三角形各边相切的不同情况,利用勾股定理列方程求出圆的半径,找出正确的答案.
解答 解:①∵⊙O是△ABC的内切圆,
∴⊙O的半径=$\frac{a+b-c}{2}$,
∴A不正确;
②∵⊙O与AB,BC相切,
∴r2+(c-a)2=(b-r)2
∴r=$\frac{(a+b-c)(b+c-a)}{2b}$,
∴B不正确;
③∵⊙O与AC,BC相切,圆心在AB上,
∴$\frac{b=r}{b}$=$\frac{r}{a}$,
∴r=$\frac{ab}{a+b}$,
∴C正确,
④∵⊙O与AB,AC相切,圆心在BC 上,
∴(a-r)2=r2+(c-b)2,
∴r=$\frac{(a+c-b)(a-c+b)}{2a}$,
∴D不正确.
点评 本题考查了三角形的内切圆,切线长定理,勾股定理的应用,正确弄清圆与三角形的位置关系是解决本题的关键.

练习册系列答案
相关题目
8.在平面直角坐标系中,将点A(-3,4)向右平移5个单位长度后,那么平移后对应的点A′的坐标是( )
| A. | (-3,-4) | B. | (2,4) | C. | (-3,9) | D. | (2,-1) |
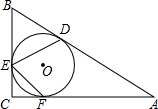 如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为80°.
如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为80°.