题目内容
9.已知二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2)交x轴于A、B两点,交y轴于C,则:①b=-2;②c>0;③当x>1时,y随x的增大而增大;④若a=1,则△ABC是直角三角形.以上说法正确的有( )| A. | ①② | B. | ①③ | C. | ①④ | D. | ②④ |
分析 ①二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2),因而将M、N两点坐标代入即可消去a、c解得b值.
②二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2),因而将M、N两点坐标代入即可消去b解得a=-c>0.
③求出对称轴,然后结合a的取值范围判断.
④根据交点坐标与系数的关系可以判断.
解答 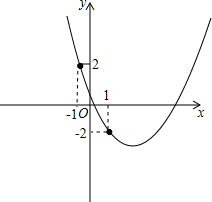 解:∵二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2),
解:∵二次函数y=ax2+bx+c(a>0)经过点M(-1,2)和点N(1,-2),
∴$\left\{\begin{array}{l}{2=a-b+c(i)\\}\\{-2=a+b+c(ii)}\end{array}\right.$,
由(i)-(ii)得到:b=-2,故①正确;
由(i)-(ii)得到a+c=0,则a=-c>0,所以c<0.故②错误;
二次函数y=ax2+bx+c(a>0)的对称轴x=-$\frac{b}{2a}$=$\frac{2}{a}$,当a>0时不能判定x>1时,y随x的增大而减小;故③错误;
④∵a=1,
∴二次函数为y=x2-2x+c,
∴C(0,c),
由根与系数可知OA•OB=|c|=OC.
∴AB2=|(x1+x2)2-4x1•x2|=|(-2)2-4c|=|4-4c|.
AC2+BC2=|x12+c2+x22+c2|=|(x1+x2)2-2x1•x2+2c2|=|4-2c+2c2|.
故④正确.
故选:C.
点评 本题考查了抛物线与x轴的交点,交点坐标和系数的关系,熟悉抛物线的对称性及抛物线与x轴的交点坐标是本题的关键.

练习册系列答案
相关题目
17.我国是一个严重缺水的国家,淡水资源总量为28000亿立方米,人均淡水资源低于世界平均水平,因此,珍惜水、保护水是我们每一位公民的责任,其中数据28000用科学记数法表示为( )
| A. | 28×103 | B. | 2.8×104 | C. | 0.28×105 | D. | 2.8×105 |
19.某学校在开展“节约每一滴水”的活动中,从初三年级的360名同学中随机选出20名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:
用所学的统计知识估计这360名同学的家庭一个月节约用水的总量大约是540吨.
| 节水量(单位:吨) | 1 | 1.2 | 1.5 | 2 | 2.5 |
| 同学数 | 4 | 5 | 6 | 3 | 2 |
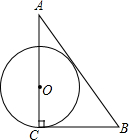
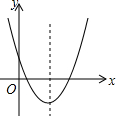 二次函数的图象如图所示,其对称轴为x=$\frac{3}{2}$,A(2,y1),B($\frac{4}{3}$,y2)两点均在二次函数的图象上,则y1与y2的大小关系为y1>y2.
二次函数的图象如图所示,其对称轴为x=$\frac{3}{2}$,A(2,y1),B($\frac{4}{3}$,y2)两点均在二次函数的图象上,则y1与y2的大小关系为y1>y2.