题目内容
8.已知平行四边形ABCD的两邻边AB、AD的长是关于x的一元二次方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.(1)当m为何值时,四边形ABCD是菱形;
(2)求出此时菱形的边长.
分析 (1)根据题意△=0,构建方程,解方程即可.
(2)把m=1代入方程,解方程即可解决问题.
解答 解:(1)四边形ABCD为菱形,则方程有两个相等的实数根,
∴△=b2-4ac=(-m)2-4($\frac{m}{2}$-$\frac{1}{4}$)=0,
即m2-2m+1=0,
解得 m=1,
所以当m=1时,四边形ABCD为菱形.
(2)把m=1代入原方程得x2-x+$\frac{1}{4}$=0,
解得 ${x_1}={x_2}=\frac{1}{2}$
所以菱形的边长为$\frac{1}{2}$.
点评 本题考查菱形的性质、一元二次方程的解、根的判别式等知识,解题的关键是熟练掌握基本知识,用转化的思考思考问题,属于中考常考题型.

练习册系列答案
相关题目
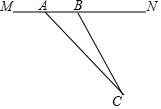 目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)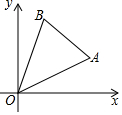 如图,在平面直角坐标系中,点A(a,b),B(c,a)均在第一象限,且c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$(b<a<3b)
如图,在平面直角坐标系中,点A(a,b),B(c,a)均在第一象限,且c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$(b<a<3b) 如图,已知OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=2,则点P到OB的距离为2.
如图,已知OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=2,则点P到OB的距离为2.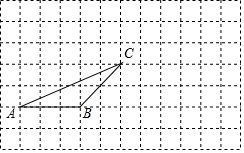 (1)过点A画出BC的平行线;
(1)过点A画出BC的平行线;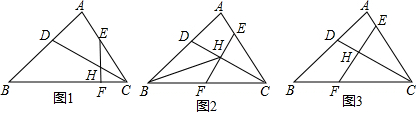
 数学活动课上,老师组织学生测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面还多1米,当同学们把绳子的下端拉开5米后,发现绳子下端刚好接触地面,请你根据题意画出图形,并求旗杆的高度.
数学活动课上,老师组织学生测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子垂到了地面还多1米,当同学们把绳子的下端拉开5米后,发现绳子下端刚好接触地面,请你根据题意画出图形,并求旗杆的高度.