题目内容
5.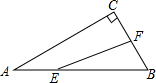 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC的中点.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t≤3),连接EF,当t为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s时,△BEF是直角三角形.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC的中点.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t≤3),连接EF,当t为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s时,△BEF是直角三角形.
分析 先利用含30度的直角三角形三边的关系得到AC=2$\sqrt{3}$,AB=4,然后讨论:当∠BFE=90°时,则EF∥AC,则可利用EF为△ABC的中位线得到AE=$\frac{1}{2}$AB=2,于是可计算出t=1(s)或t=3(s);当∠FEB=90°,则证明△BEF∽△BCA,利用相似比可计算出BE=$\frac{1}{2}$,则AE=$\frac{7}{2}$,于是可计算出t=$\frac{7}{4}$(s)或t=$\frac{9}{4}$(s).
解答 解:∵∠ACB=90°,∠ABC=60°,BC=2cm,
∴AC=$\sqrt{3}$BC=2$\sqrt{3}$,AB=2BC=4,
当∠BFE=90°时,则EF∥AC,
∵F是BC的中点,
∴EF为△ABC的中位线,
∴AE=$\frac{1}{2}$AB=2,
∴t=$\frac{2}{2}$=1(s)或t=$\frac{4+2}{2}$=3(s);
当∠FEB=90°,
∵∠FBE=∠ABC,∠BEF=∠C,
∴△BEF∽△BCA,
∴$\frac{BE}{BC}$=$\frac{BF}{BA}$,即$\frac{BE}{2}$=$\frac{1}{4}$,解得BE=$\frac{1}{2}$,
∴AE=4-$\frac{1}{2}$=$\frac{7}{2}$,
∴t=$\frac{\frac{7}{2}}{2}$=$\frac{7}{4}$(s)或t=$\frac{4+\frac{1}{2}}{2}$=$\frac{9}{4}$(s),
综上所述,t的值为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s.
故答案为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用相似三角形的性质时,主要利用相似比计算线段的长.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案
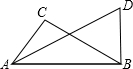 如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,试求BC的长.
如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,试求BC的长.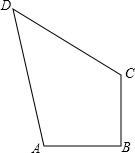 如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( ) 一块钢板形状如图所示,量得AB=3,BC=4,AC=5,CD=12,AD=13,请你计算一下这块钢板的面积.
一块钢板形状如图所示,量得AB=3,BC=4,AC=5,CD=12,AD=13,请你计算一下这块钢板的面积.