题目内容
8. 如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )| A. | $\frac{3}{2}$ | B. | 4 | C. | $\frac{5}{2}$ | D. | 1 |
分析 根据三角形中位线定理得到DE=$\frac{1}{2}$BC=4,根据直角三角形的性质得到DF=$\frac{1}{2}$AB=$\frac{5}{2}$,计算即可.
解答 解:∵DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC=4,DE∥BC,
∵∠AFB=90°,D为AB的中点,
∴DF=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴EF=DE-DF=$\frac{3}{2}$,
故选:A.
点评 本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半和在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
13.下列说法不正确的是( )
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{2}$是2的算术平方根 | D. | 3是$\sqrt{(-3)^{2}}$的平方根 |
18.下列各数中,不属于正数的是( )
| A. | -0.2 | B. | 5.5 | C. | $\frac{1}{5}$ | D. | 20 |
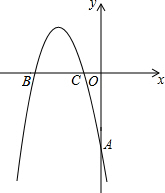 如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c,经过A(0,-4)、它的对称轴为 x=-$\frac{7}{2}$,它与x轴相交于B、C.
如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c,经过A(0,-4)、它的对称轴为 x=-$\frac{7}{2}$,它与x轴相交于B、C.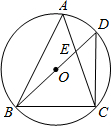 已知如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,BD=10,BD交AC于点E,连接DC.
已知如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,BD=10,BD交AC于点E,连接DC.