题目内容
1. 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
分析 (1)将D(-4,0),B(0,4)代入y=-x2+bx+c,运用待定系数法即可求出抛物线的解析式;
(2)先求出抛物线与直线BC的交点为(-2,4)(0,4),得出点P在直线BC上方时,m的取值范围,再根据P(m,-m2-3m+4),G(m,4),求出PG=-m2-m;
(3)先由DO∥BC,得到$\frac{BG}{DE}=\frac{GH}{HE}$,表示出BG=GH=-m,HE=DE=4+m,从而判断出只有△PGB∽△DEH,得到比例式求解即可.
解答 解:(1)∵四边形OBCD是正方形,点B坐标为(0,4),
∴D点的坐标是(-4,0),
∵点B和点D在抛物线上
∴$\left\{\begin{array}{l}{c=4}\\{-16-4b+c}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-3}\\{c=4}\end{array}\right.$,
∴该抛物线的解析式为:y=-x2-3x+4;
(2)∵4=-m2-3m+4,解得m=-3或0,
∴抛物线与直线BC的交点为(-3,4)(0,4),
∴点P在直线BC上方时,m的取值范围是:-3<m<0,
∵E(m,0),B(0,4),
∵PE⊥x轴交抛物线于点P,交BC于点G,
∴P(m,-m2-3m+4),G(m,4),
∴PG=-m2-3m+4-4=-m2-3m,
(3)∵抛物线的解析式为:y=-x2-3x+4;
设点P(m,-m2-3m+4),
∴BG=m,DE=m+4,
∵DO∥BC,
∴$\frac{BG}{DE}=\frac{GH}{HE}$,
∵GH=4,
∴BG=GH=-m,HE=DE=4+m,
∵以P、B、G为顶点的三角形与△DEH相似且∠PGB=∠DEH=90°,
∴△PGB∽△DEH,
∴$\frac{PG}{DE}=\frac{GB}{HE}$,
∴GB=PG,
∴-m=-m2-3m,
∴m=2或m=0(舍)
即:m=2
点评 此题是二次函数综合题,主要考查了二次函数的综合,其中涉及到运用待定系数法求二次函数、线段的表示、正方形的性质等知识,综合性较强,运用数形结合、方程思想是解题的关键.

| A. | 321×103米 | B. | 32.1×103米 | C. | 3.21×104米 | D. | 3.21×103米 |
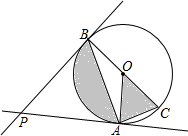 如图,PA、PB与⊙O相切,切点分别为A、B,PA=3,∠BPA=60°,若BC为⊙O的直径,则图中阴影部分的面积为( )
如图,PA、PB与⊙O相切,切点分别为A、B,PA=3,∠BPA=60°,若BC为⊙O的直径,则图中阴影部分的面积为( )| A. | 3π | B. | π | C. | 2π | D. | $\frac{π}{2}$ |
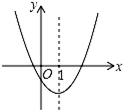 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论:
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论: 如图,平行四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.△ABD的周长为8cm,则△DOE的周长是4cm.
如图,平行四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.△ABD的周长为8cm,则△DOE的周长是4cm.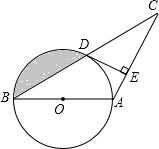 已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E. 如图,在?ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.
如图,在?ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.