题目内容
4.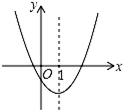 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论:
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论:①b2>4ac;
②4a-2b+c<0;
③b<-2c;
④若点(-2,y1)与(5,y2)是抛物线上的两点,则y1<y2,
其中,正确的结论有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据图象与x轴有2个交点,确定b2-4ac>0,即可判断①;根据当x=-2时,y的符号确定4a-2b+c的符号,即可判断②;由抛物线与y轴的交点判断c与0的关系,然后根据对称轴确定b的符号,即可判断③;根据二次函数的增减性判断④.
解答 解:图象与x轴有2个交点,依据根的判别式可知b2-4ac>0,b2>4ac,①正确;
当x=-2时,不能确定y的符号,∴4a-2b+c的符号不能确定,②不正确;
由-$\frac{b}{2a}$=1,又a>0,∴b<0,图象与y轴交于负半轴,∴c<0,∴b<-2c,③正确;
由对称轴为x=1,当x=-2时和x=4时,函数值相等,根据函数性质,x=5的函数值大于x=4的函数值,∴y1<y2,④正确.
故选:C.
点评 考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14. 如图,等边△ABC内接于⊙O,BC=4,PC切⊙O于C,AP⊥CP,则BP的长为( )
如图,等边△ABC内接于⊙O,BC=4,PC切⊙O于C,AP⊥CP,则BP的长为( )
 如图,等边△ABC内接于⊙O,BC=4,PC切⊙O于C,AP⊥CP,则BP的长为( )
如图,等边△ABC内接于⊙O,BC=4,PC切⊙O于C,AP⊥CP,则BP的长为( )| A. | 5 | B. | 6 | C. | 2$\sqrt{7}$ | D. | 2$\sqrt{6}$ |
12.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.6环,方差分别是S甲2=0.96,S乙2=1.12,S丙2=0.56,S丁2=1.58.在本次射击测试中,成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
19.据报道,截至2015年12月底,我区户籍人口突破90万.数据“90万”用科学记数法可表示为( )
| A. | 90×104 | B. | 9×104 | C. | 9×105 | D. | 0.9×105 |
5.菱形具有而矩形不一定具有的性质是( )
| A. | 内角和等于360° | B. | 对角相等 | C. | 对角线互相垂直 | D. | 对边平行且相等 |
 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H. 如图,AB是⊙O的直径,点C在⊙O上(点C不与A、B重合),过点C作⊙O的切线交AB的延长线于点D,连结AC.若∠A=25°,则∠D的度数是40°°.
如图,AB是⊙O的直径,点C在⊙O上(点C不与A、B重合),过点C作⊙O的切线交AB的延长线于点D,连结AC.若∠A=25°,则∠D的度数是40°°.