题目内容
 如图,一艘轮船自西向东航行,在点A处测得北偏东68.7°方向有一座小岛C,继续向东航行80海里后到达点B处,此时测得小岛C在船的北偏东26.5°方向上,然后轮船继续向东航行多少海里,距离小岛C最近?(参考数据:sin21.3°≈
如图,一艘轮船自西向东航行,在点A处测得北偏东68.7°方向有一座小岛C,继续向东航行80海里后到达点B处,此时测得小岛C在船的北偏东26.5°方向上,然后轮船继续向东航行多少海里,距离小岛C最近?(参考数据:sin21.3°≈| 9 |
| 25 |
| 2 |
| 5 |
| 9 |
| 10 |
考点:解直角三角形的应用-方向角问题
专题:
分析:根据题意tan∠A=
=
,CD=
(80+BD),由tan63.5°=
≈2,得出CD=2BD,进而求出BD即可.
| CD |
| AD |
| 2 |
| 5 |
| 2 |
| 5 |
| CD |
| BD |
解答: 解:过点C作CD⊥AB,垂足为点D,此时轮船离小岛最近,BD即为所求,
解:过点C作CD⊥AB,垂足为点D,此时轮船离小岛最近,BD即为所求,
由题意可知:∠A=21.3°,AB=80海里,∠CBD=63.5°,
在Rt△ACD中,tan∠A=
=
,CD=
(80+BD),
∵tan63.5°=
≈2,
∴CD=2BD,
故2BD=
(80+BD),
解得:BD=20.
答:轮船继续向东航行20海里,距离小岛C最近.
 解:过点C作CD⊥AB,垂足为点D,此时轮船离小岛最近,BD即为所求,
解:过点C作CD⊥AB,垂足为点D,此时轮船离小岛最近,BD即为所求,由题意可知:∠A=21.3°,AB=80海里,∠CBD=63.5°,
在Rt△ACD中,tan∠A=
| CD |
| AD |
| 2 |
| 5 |
| 2 |
| 5 |
∵tan63.5°=
| CD |
| BD |
∴CD=2BD,
故2BD=
| 2 |
| 5 |
解得:BD=20.
答:轮船继续向东航行20海里,距离小岛C最近.
点评:此题主要考查了方向角问题,得出CD与BD的关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设m>n>0,m2+n2=3mn,则
的值等于( )
| m2-n2 |
| mn |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
 将两个全等的直角三角形,拼成一个四边形.问:这些四边形中有几个轴对称图形,有几个中心对称图形?
将两个全等的直角三角形,拼成一个四边形.问:这些四边形中有几个轴对称图形,有几个中心对称图形? 已知:如图,线段a,
已知:如图,线段a, 如图,正方形网格中,有格点三角形△ABC(顶点都是格点)和直线l.
如图,正方形网格中,有格点三角形△ABC(顶点都是格点)和直线l.
 在Rt△ABC中,∠C=90°,点D为BC边上一点,CD=1,且cos∠ADC=
在Rt△ABC中,∠C=90°,点D为BC边上一点,CD=1,且cos∠ADC=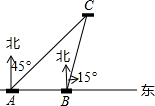 如图,某日我国某岛附近海域有两艘自西向东航行的海监船A、B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
如图,某日我国某岛附近海域有两艘自西向东航行的海监船A、B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)