题目内容
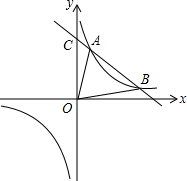 一次函数y1=ax+3与反比例函数y2=
一次函数y1=ax+3与反比例函数y2=| b+1 |
| x |
(1)确定这两个函数的表达式;
(2)若y1>y2,求x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A点坐标分别代入两函数解析式可求得这两个函数的表达式;
(2)先求得B点坐标,当一次函数图象在反比例函数图象上方时,满足条件,结合图象可求得x的取值范围.
(2)先求得B点坐标,当一次函数图象在反比例函数图象上方时,满足条件,结合图象可求得x的取值范围.
解答:解:(1)∵A为两函数图象的交点,
∴2=a+3,b+1=2,
解得a=-1,b=1,
∴y1=-x+3,y2=
;
(2)联立两函数解析式可得
,
解得
或
,
∴B点坐标为(2,1),
由图象可知当x<0或1<x<2时,正比例函数图象在反比例函数图象的上方,
∴当y1>y2时,x的取值范围为x<0或1<x<2.
∴2=a+3,b+1=2,
解得a=-1,b=1,
∴y1=-x+3,y2=
| 2 |
| x |
(2)联立两函数解析式可得
|
解得
|
|
∴B点坐标为(2,1),
由图象可知当x<0或1<x<2时,正比例函数图象在反比例函数图象的上方,
∴当y1>y2时,x的取值范围为x<0或1<x<2.
点评:本题主要考查待定系数法求函数解析式,掌握两函数图象的交点坐标满足每个函数解析式是解题的关键.

练习册系列答案
相关题目
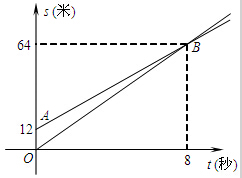 如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法:
如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法: 如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①abc>0;②4a+c<2b;③4ac-b2<0;④3b+2c<0,其中正确信息的个数是( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①abc>0;②4a+c<2b;③4ac-b2<0;④3b+2c<0,其中正确信息的个数是( ) 一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点.
一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点.
 如图,点C和点D在线段AB上,AE∥BF,AE=FB,AC=DB,连接EC、ED、FC、FD.
如图,点C和点D在线段AB上,AE∥BF,AE=FB,AC=DB,连接EC、ED、FC、FD. 如图,⊙O的两弦AB,CD垂直相交于点E,试判断∠AOC与∠?BOD的关系并给出证明.
如图,⊙O的两弦AB,CD垂直相交于点E,试判断∠AOC与∠?BOD的关系并给出证明.