题目内容
 如图所示,小岛P的周围20
如图所示,小岛P的周围20| 2 |
考点:解直角三角形的应用-方向角问题
专题:
分析:作PB⊥AM,求出PB的长即可判断是否触礁,作⊙P的切线AE,切点为E,利用三角函数即可求出∠PAE,从而得到渔船在A处应再向北偏东至少偏离多大角度才能脱险.
解答: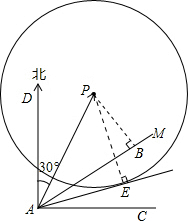 解:作PB⊥AM.
解:作PB⊥AM.
∵∠DAB=61°,∠DAP=30°,
∴∠PAB=61°-30°=31°,
∴PB=AP•sin31°≈20.6(海里)<20
(海里),
作⊙P的切线AE,切点为E.
∴sin∠PAE=
=
,
∴∠PAE=45°.
答:有可能触礁,该渔船在A处应再向北偏东至少偏离45°才能脱离危险.
 解:作PB⊥AM.
解:作PB⊥AM.∵∠DAB=61°,∠DAP=30°,
∴∠PAB=61°-30°=31°,
∴PB=AP•sin31°≈20.6(海里)<20
| 2 |
作⊙P的切线AE,切点为E.
∴sin∠PAE=
20
| ||
| 40 |
| ||
| 2 |
∴∠PAE=45°.
答:有可能触礁,该渔船在A处应再向北偏东至少偏离45°才能脱离危险.
点评:本题考查了解直角三角形--方向角问题,根据题意构造直角三角形是解题的关键.

练习册系列答案
相关题目
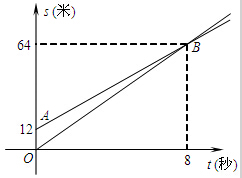 如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法:
如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法: 如图,点C和点D在线段AB上,AE∥BF,AE=FB,AC=DB,连接EC、ED、FC、FD.
如图,点C和点D在线段AB上,AE∥BF,AE=FB,AC=DB,连接EC、ED、FC、FD. 如图:
如图: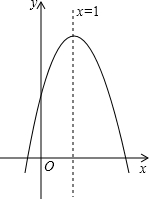 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的个数是( ) 如图,⊙O的两弦AB,CD垂直相交于点E,试判断∠AOC与∠?BOD的关系并给出证明.
如图,⊙O的两弦AB,CD垂直相交于点E,试判断∠AOC与∠?BOD的关系并给出证明. 如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积是多少?
如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积是多少?