题目内容
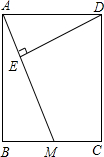 如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.
如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.考点:矩形的性质
专题:
分析:由矩形ABCD中,AB=12cm,BC=10cm,M为BC的中点,由勾股定理可求得AM的长,又由DE⊥AM,易证得△ADE∽△MAB,然后由相似三角形的对应边成比例,求得DE的长.
解答:解:∵四边形ABCD是矩形,
∴∠B=90°,∠DAE=∠AMB,
∵DE⊥AM,
∴∠ADE=∠B=90°,
∴△ADE∽△MAB,
∵M 是BC中点,BC=10cm,
∴BM=5cm,
根据勾股定理得AM=13cm,
∵△ADE∽△MAB,
∴DE:AB=AD:AM,
即DE:12=10:13,
∴DE=
cm.
∴∠B=90°,∠DAE=∠AMB,
∵DE⊥AM,
∴∠ADE=∠B=90°,
∴△ADE∽△MAB,
∵M 是BC中点,BC=10cm,
∴BM=5cm,
根据勾股定理得AM=13cm,
∵△ADE∽△MAB,
∴DE:AB=AD:AM,
即DE:12=10:13,
∴DE=
| 120 |
| 13 |
点评:此题考查了相似三角形的判定与性质、矩形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
2013年12月15日,“玉兔号”月球车月面软着陆后离地球380000千米,能够看到地球等离子层的全貌.380000千米用科学记数法表示为( )
| A、38×107米 |
| B、3.8×108米 |
| C、3.8×109米 |
| D、0.38×109米 |
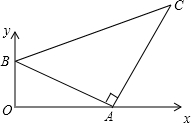 如图,直线AB分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,点A的坐标为(4,0),点B的坐标为(0,2),求C点的坐标.
如图,直线AB分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,点A的坐标为(4,0),点B的坐标为(0,2),求C点的坐标. 如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.
如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.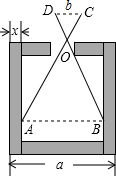 如图,已知零件的外径a=35cm,要求它的厚度x,需先求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(两条尺长AC和BD相等)测量,已知OA:OC=OB:OD=3,且量得CD=10cm,求厚度x.
如图,已知零件的外径a=35cm,要求它的厚度x,需先求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(两条尺长AC和BD相等)测量,已知OA:OC=OB:OD=3,且量得CD=10cm,求厚度x.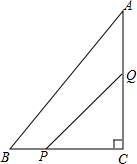 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?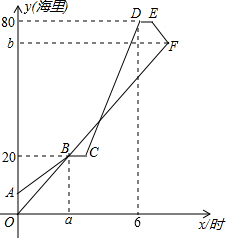 在距离港口80海里处,有一艘渔船发出求救信息,甲、乙两艘救援船同时接到救援任务,甲船立即出发,乙船因需要等候救援家属,在甲救援船驶离港口5海里时才出发.乙船以10海里/小时的速度匀速行驶,甲船途中因故障维修停船1小时,然后提高速度匀速行驶,到达目的地救援1小时后原路匀速返回与乙船相遇,甲船返回时的速度与提高后的速度相同,图中折线AB-BC-CD-DE-EF,线段OF分别表示甲、乙两船与港口的距离y(海里)与乙船出发时间x(时)之间的图象.
在距离港口80海里处,有一艘渔船发出求救信息,甲、乙两艘救援船同时接到救援任务,甲船立即出发,乙船因需要等候救援家属,在甲救援船驶离港口5海里时才出发.乙船以10海里/小时的速度匀速行驶,甲船途中因故障维修停船1小时,然后提高速度匀速行驶,到达目的地救援1小时后原路匀速返回与乙船相遇,甲船返回时的速度与提高后的速度相同,图中折线AB-BC-CD-DE-EF,线段OF分别表示甲、乙两船与港口的距离y(海里)与乙船出发时间x(时)之间的图象.