题目内容
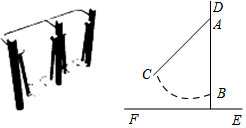
10. 已知,如图,AC⊥BC,BD⊥BC,AC>BC>BD.
已知,如图,AC⊥BC,BD⊥BC,AC>BC>BD.(1)请你添加一个条件,使△ABC相似于△CDB,你添加的条件是∠A=∠D(答案不唯一);
(2)若DB=3,BC=4,在(1)的条件下,求AC的长度.
分析 (1)根据相似三角形的判定定理即可得出结论;
(2)根据相似三角形的性质即可得出结论.
解答 解:(1)∵AC⊥BC,BD⊥BC,
∴∠ACB=∠CBD,
∴可以添加的条件是∠A=∠D.
故答案为:∠A=∠D(答案不唯一);
(2)∵△ABC∽△CDB,DB=3,BC=4,
∴$\frac{AC}{BC}$=$\frac{BC}{DB}$,即$\frac{AC}{4}$=$\frac{4}{3}$,
解得AC=$\frac{16}{3}$.
点评 本题考查的是相似三角形的判定,熟知有两组角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
相关题目
15.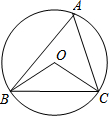 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 4 |
20.下列各组数不可能是一个三角形的边长的是( )
| A. | 5,5,5 | B. | 5,7,7 | C. | 5,12,13 | D. | 5,7,12 |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.