题目内容
7. 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为$\frac{\sqrt{2}}{2}$.
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为$\frac{\sqrt{2}}{2}$.
分析 设Q是AB的中点,连接DQ,先证得△AQD≌△AOE,得出QD=OE,根据点到直线的距离可知当QD⊥BC时,QD最小,然后根据等腰直角三角形的性质求得QD⊥BC时的QD的值,即可求得线段OE的最小值.
解答 解:设Q是AB的中点,连接DQ,
∵∠BAC=∠DAE=90°,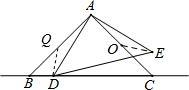
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
∵AB=AC=2,O为AC中点,
∴AQ=AO,
在△AQD和△AOE中,
$\left\{\begin{array}{l}{AQ=AO}\\{∠QAD=∠OAE}\\{AD=AC}\end{array}\right.$,
∴△AQD≌△AOE(SAS),
∴QD=OE,
∵点D在直线BC上运动,
∴当QD⊥BC时,QD最小,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵QD⊥BC,
∴△QBD是等腰直角三角形,
∴QD=$\frac{\sqrt{2}}{2}$QB,
∵QB=$\frac{1}{2}$AB=1,
∴QD=$\frac{\sqrt{2}}{2}$,
∴线段OE的最小值是为 $\frac{\sqrt{2}}{2}$.
故答案为$\frac{\sqrt{2}}{2}$.
点评 本题考查了等腰直角三角形的性质、三角形全等的判定和性质、垂线段最短等知识,作出辅助线构建全等三角形是解题的关键.

练习册系列答案
相关题目
2. 如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( )
如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( )
 如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( )
如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( )| A. | 20° | B. | 35° | C. | 130° | D. | 140° |
12.初二(1)班为元旦文艺表演者发奖,用一定数量的钱去买奖品,若以1支钢笔和2个笔记本为一份奖品,正好能买60份;若以1支钢笔和3本笔记本为一份奖品,正好能买50份;若以1支钢笔和1个笔记本为一份奖品,则这笔钱能买( )份.
| A. | 80 | B. | 70 | C. | 75 | D. | 55 |
19.下列语句叙述不正确的是( )
| A. | 若上升3米记作+3米,则不升不降记为0米 | |
| B. | 水位的变化是-2米,表示的意义是水位下降了-2米 | |
| C. | 温度上升-10℃是指下降10℃ | |
| D. | 盈利-10元是指亏损10元 |
17.从分别标有数字-3,-2,-1,0,1,2,3的七张卡片中,随机抽取一张,所抽卡片上数字的绝对值不大于2的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
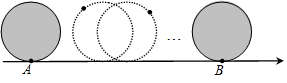 如图,半径为1个单位长度的圆从点A沿数轴向右滚动(无滑动)一周到达点B,则AB的长度为π;若点A对应的数是-1,则点B对应的数是π-1.
如图,半径为1个单位长度的圆从点A沿数轴向右滚动(无滑动)一周到达点B,则AB的长度为π;若点A对应的数是-1,则点B对应的数是π-1.